
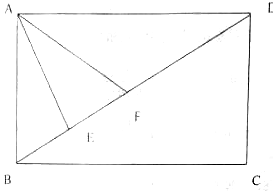
 С����ѧ��ҵ�����������ѧ֪ʶ������ҵ����һ����εĿյ��ϰ�������ֳ������ͼ��ʾ���ı���ABCDΪ���Σ�AB=200�ף�AD=200$\sqrt{3}$�ף���Ϊ����ֳ��Ҫ������ֳ����Ҫ������ˮ�أ�С��������ˣ�������һ����������״����ˮ�أ����ж���ֱ�ΪA��E��F��E��F�������߶�BD�ϣ����ҡ�EAF=$\frac{��}{6}$�����BAE=����
С����ѧ��ҵ�����������ѧ֪ʶ������ҵ����һ����εĿյ��ϰ�������ֳ������ͼ��ʾ���ı���ABCDΪ���Σ�AB=200�ף�AD=200$\sqrt{3}$�ף���Ϊ����ֳ��Ҫ������ֳ����Ҫ������ˮ�أ�С��������ˣ�������һ����������״����ˮ�أ����ж���ֱ�ΪA��E��F��E��F�������߶�BD�ϣ����ҡ�EAF=$\frac{��}{6}$�����BAE=�������� ��1����������ķ�Χ���ٷֱ�������Ҷ����õ�AE��AF���ٸ��������ε������ʽ���ɱ�ʾ��f��������
��2���������Һ�����ͼ������ʼ��������ֵ��
��� �⣺��1���ߡ�BCD=$\frac{��}{2}$����EAF=$\frac{��}{6}$�����BAE=����[0��$\frac{��}{3}$]��
�ڡ�ABD�У�AD=200�ף�AD=200$\sqrt{3}$�ף���BCD=$\frac{��}{2}$��
���ABD=$\frac{��}{3}$��
�ڡ�ABF�У���AFB=��-��ABF-��BAF=��-$\frac{��}{3}$-��$\frac{��}{6}$+����=$\frac{��}{2}$-����
�����Ҷ����ã�$\frac{AF}{sin��ABF}$=$\frac{AB}{sin��AFB}$=$\frac{AB}{sin��\frac{��}{2}-����}$=$\frac{AB}{cos��}$��
��AF=$\frac{100\sqrt{3}}{cos��}$��
�ڡ�ABE�У������Ҷ����ã�$\frac{AE}{sin��ABE}$=$\frac{AB}{sin��AEB}$=$\frac{AB}{sin��\frac{��}{3}+����}$��
��AE=$\frac{100\sqrt{3}}{sin��\frac{��}{3}+����}$��
���AEF�����S��AEF=$\frac{1}{2}$AE•AF•sin��EAF=$\frac{7500}{sin��\frac{��}{3}+����cos��}$=$\frac{3000}{2sin��2��+\frac{��}{3}��+\sqrt{3}}$������[0��$\frac{��}{3}$]��
��f������=$\frac{3000}{2sin��2��+\frac{��}{3}��+\sqrt{3}}$������[0��$\frac{��}{3}$]��
��2���ߦ���[0��$\frac{��}{3}$]��
�ࣨ2��+$\frac{��}{3}$����[$\frac{��}{3}$����]��
��0��sin��2��+$\frac{��}{3}$����1��
��2sin��2��+$\frac{��}{3}$��+$\sqrt{3}$����СֵΪ$\sqrt{3}$��
�൱��=$\frac{��}{3}$ʱ��f������max=1000$\sqrt{3}$
���� ���⿼�������Ҷ������Լ������ε������ʽ�����Һ�����ͼ������ʣ�������ѧ����������������������������е���


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Բ���е��������ȫ�ȵĵ��������� | |
| B�� | Բ����������ǹ�ĸ�ߵĽ������������һ�� | |
| C�� | Բ������������й�����Ľ������������һ�� | |
| D�� | �����ĵ�ƽ��ľ���С������뾶ʱ��������ƽ��Ľ�������һ��Բ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
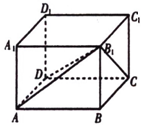 �ڳ�����ABCD-A1B1C1D1����ȡ�㣬��õ���������B1-ABCD�ڲ��ĸ�����$\frac{1}{3}$��
�ڳ�����ABCD-A1B1C1D1����ȡ�㣬��õ���������B1-ABCD�ڲ��ĸ�����$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{6}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{��}{3}��\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com