
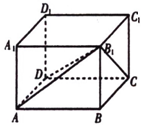
 在长方体ABCD-A1B1C1D1任意取点,则该点落在四棱锥B1-ABCD内部的概率是$\frac{1}{3}$.
在长方体ABCD-A1B1C1D1任意取点,则该点落在四棱锥B1-ABCD内部的概率是$\frac{1}{3}$.  名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0秒、2秒或4秒 | B. | 0秒、2秒或16秒 | C. | 0秒、4秒或8秒 | D. | 2秒、8秒或16秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
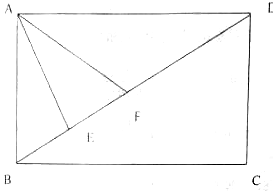 小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.
小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com