
分析 (1)求出函数的导数,得到关于a,b的方程组,求出a,b的值即可;(2)求出函数的导数,根据函数的单调性求出f(x)的最小值,求出c的范围即可.
解答 解:(1)$f'(x)=2a+\frac{b}{x^2}+\frac{4}{x}$$f(x)=2ax-\frac{b}{x}+4lnx$,
在$x=1与x=\frac{1}{3}$处都取得极值,
$\begin{array}{l}f'(1)=0,f'(\frac{1}{3})=0\\∴\left\{\begin{array}{l}2a+b+4=0\\ 2a+9b+12=0\end{array}\right.\end{array}$,
解得:a=-$\frac{3}{2}$,b=-1; 经检验符合题意;
(2)由(1)可知,$f(x)=-3x+\frac{1}{x}+4lnx$,
$f'(x)=-3-\frac{1}{x^2}+\frac{4}{x}=-\frac{(3x-1)(x-1)}{x^2}$,
由f'(x)>0,得f(x)的单调增区间为[$\frac{1}{3}$,1],
由f'(x)<0,得f(x)的单调减区间为$(0,\frac{1}{3}]和[1,+∞)$,
∴x=1是f(x)的极大值点 当$x∈[\frac{1}{e},e]$时,$f(\frac{1}{e})$=e-$\frac{3}{e}$-5,f(e)=-3e+$\frac{1}{e}$+4,
而$f(\frac{1}{e})$-f(e)=4e-9-$\frac{4}{e}$>0,所以$f(\frac{1}{e})$>f(e),
即f(x)在$x∈[\frac{1}{e},e]$上的最小值为$\frac{1}{e}$+4-3e,
要使对$x∈[\frac{1}{e},e]$时,f(x)≥c恒成立,
故$c≤f{(x)_{min}}=\frac{1}{e}+4-3e$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
| A. | 做米饭需要刷锅,淘米,添水,加热这些步骤 | |
| B. | 洗衣机的使用说明书 | |
| C. | 利用公式S=πr2计算半径为4的圆的面积,就是计算π×42 | |
| D. | 解方程2x2+x-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | $-\frac{3}{8}$ | C. | 6 | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
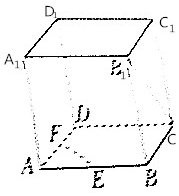 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
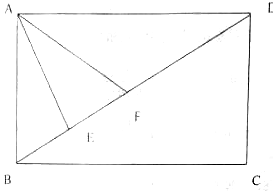 小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.
小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com