
【题目】设双曲线![]() 的两支为
的两支为![]() (如图),正三角形PQR的三顶点位于此双曲线上。
(如图),正三角形PQR的三顶点位于此双曲线上。

(1)求证:P、Q、R不能都在双曲线的同一支上;
(2)设P(-1,-1)在![]() 上,Q、R在
上,Q、R在![]() 上。求顶点Q、R的坐标。
上。求顶点Q、R的坐标。
【答案】(1)见解析;(2)![]() ,
,![]()
【解析】
(1)用反证法.
假设正△PQR的三顶点P、Q、R位于同一支如![]() 上,其坐示分別的
上,其坐示分別的![]() ,不妨设0
,不妨设0![]() .则一定有
.则一定有![]() .于是,
.于是,![]()
![]()
![]()
![]() .
.
因此![]() .
.
这说明△PQR是钝角三角形,与△PQR为正三角形矛盾.故P、Q、R不能位于同一支上.
(2)设Q、R的坐标为![]() ,这时QR边上的高线方程为
,这时QR边上的高线方程为![]() .
.

它必过线段QR的中点,因此QR的中点坐标满足方程(1),
于是有![]() .此即
.此即 ![]() ..
..
![]() ,上式方括号中的式子明显大于0,则
,上式方括号中的式子明显大于0,则![]() .故
.故![]() .
.
于是,Q的坐标为![]() .而R的坐标为
.而R的坐标为![]() ,这说明Q、R关于直线y=x对称.
,这说明Q、R关于直线y=x对称.
PQ、PR所在的直线分别为过P点与y=x交成30°角的相互对称的两条直线,易见其倾斜角分别为75°和15°.不妨设PQ的倾斜角为75°,这时它的方程为![]()
即 ![]() .将其代入双曲线方程
.将其代入双曲线方程![]() ,解得Q的坐标为
,解得Q的坐标为![]() ,由对称性知R的坐标为
,由对称性知R的坐标为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,把圆
,把圆![]() 上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,且倾斜角为
,且倾斜角为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)当![]() 时,求曲线
时,求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的参数方程;
的参数方程;
(2)求点![]() 到
到![]() 两点的距离之积的最小值.
两点的距离之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=![]() (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点P
,且经过点P![]() ,过它的左、右焦点
,过它的左、右焦点![]() 分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且
分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且![]()
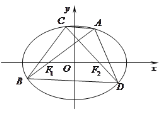
(1)求椭圆的标准方程.
(2)求四边形ACBD的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】游乐场的摩天轮匀速旋转,其中心O距地面40.5m,半径40m.若从最低点处登上座天轮,那么人与地面的距离将随时间变化,5min后达到最高点,在你登上摩天轮时开始计时,
(1)求出人与地面距离y与时间t的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于20.5m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com