设函数f(x)=x2-ax+2lnx,其中a>0
(1)当a<4时,判断函数f(x)的单调性;
(2)当a=5时,求函数f(x)的极值;
(3)证明:当x≥1时,x2+2lnx≥3x-2.
【答案】
分析:(1)求出导数f′(x),当a<4时,判断出f′(x)符号即可.
(2)当a=5时,先解f′(x)=0,再判断根左右两侧导数的符号变化,由此即可得出答案.
(3)当x≥1时,x
2+2lnx≥3x-2可变为x
2+2lnx-3x≥-2,从而问题可转化为求当a=3时f(x)在[1,+∞)的最小值问题.
解答:解:定义域为:(0,+∞),
(1)
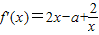
.
因为x>0,所以
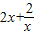
≥

=4,
又a<4,所以f'(x)>0,
故当a<4时,函数f(x)在(0,+∞)上是增函数.
(2)当a=5时,f′(x)=2x-5+
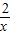
=
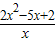
=
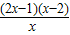
,
令f′(x)=0,得

或x=2.
当
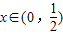
时,f'(x)>0,函数f(x)单调递增;
当
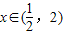
时,f'(x)<0,函数f(x)单调递减;
当x∈(2,+∞)时,f'(x)>0,函数f(x)单调递增;
由上可知,当
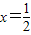
时,f(x)取极大值f(

)=
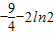
;
当x=2时,f(x)取极小值f(2)=2ln2-6.
(3)即证:当x≥1时,x
2+2lnx-3x≥-2,
由(1)知,当a=3时,f(x)=x
2+2lnx-3x在(0,+∞)上是增函数,
仅当x=1时,f(x)在区间[1,+∞)上有最小值f(1)=-2,所以当x≥1时,x
2+2lnx-3x≥-2成立,
即x
2+2lnx≥3x-2.
点评:本题考查了导数的综合应用:用导数研究函数的单调性、极值、最值问题,要深刻理解导数在研究函数中的作用.

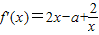 .
.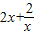 ≥
≥ =4,
=4,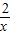 =
=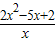 =
=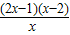 ,
, 或x=2.
或x=2.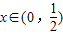 时,f'(x)>0,函数f(x)单调递增;
时,f'(x)>0,函数f(x)单调递增;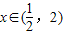 时,f'(x)<0,函数f(x)单调递减;
时,f'(x)<0,函数f(x)单调递减;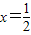 时,f(x)取极大值f(
时,f(x)取极大值f( )=
)=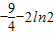 ;
;

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案