
已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.
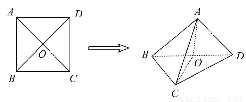
(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
(1)见解析 (2) 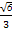
【解析】(1)根据题意,在△AOC中,AC=a=2,AO=CO=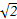 ,
,
所以AC2=AO2+CO2,所以AO⊥CO.
又AO⊥BD,BD∩CO=O,
所以AO⊥平面BCD.
(2)方法一:由(1)知,CO⊥OD,以O为原点,OC,OD所在的直线分别为x轴、y轴建立如图的空间直角坐标系Oxyz,
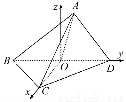
则有O(0,0,0),D(0,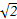 ,0),
,0),
C(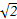 ,0,0),B(0,-
,0,0),B(0,-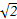 ,0).
,0).
设A(x0,0,z0)(x0<0),
则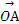 =(x0,0,z0),
=(x0,0,z0),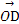 =(0,
=(0,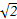 ,0).
,0).
平面ABD的一个法向量为n=(z0,0,-x0).
平面BCD的一个法向量为m=(0,0,1),且二面角A-BD-C的大小为120°,
所以|cos<m,n>|=|cos120°|=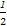 ,得
,得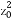 =3
=3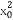 .
.
因为OA=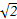 ,所以
,所以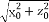 =
=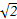 .解得x0=-
.解得x0=- ,z0=
,z0=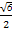 .所以A(-
.所以A(- ,0,
,0,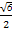 ).
).
平面ABC的一个法向量为l=(1,-1,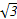 ).
).
设二面角A-BC-D的平面角为θ,
所以cosθ=|cos<l,m>|=|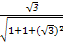 |=
|=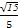 .
.
所以tanθ=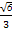 .
.
所以二面角A-BC-D的正切值为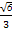 .
.
方法二:折叠后,BD⊥AO,BD⊥CO.所以∠AOC是二面角A-BD-C的平面角,即∠AOC=120°.在△AOC中,AO=CO=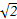 ,所以AC=
,所以AC=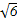 .
.
如图,过点A作CO的垂线交CO延长线于点H,
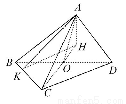
因为BD⊥CO,BD⊥AO,且CO∩AO=O,所以BD⊥平面AOC.因为AH?平面AOC,所以BD⊥AH.
又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.所以AH⊥BC.过点A作AK⊥BC,垂足为K,连接HK,因为BC⊥AH,AK∩AH=A,所以BC⊥平面AHK.因为HK?平面AHK,所以BC⊥HK.所以∠AKH为二面角A-BC-D的平面角.
在△AOH中,得AH=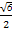 ,OH=
,OH= ,所以CH=CO+OH=
,所以CH=CO+OH=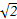 +
+ =
=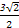 .
.
在Rt△CHK中,HK=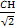 =
=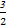 ,
,
在Rt△AHK中,tan∠AKH= =
=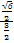 =
=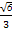 .
.
所以二面角A-BC-D的正切值为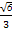 .
.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:解答题
如图,在四面体ABCD中作截面PQR,若PQ,CB的延长线交于M,RQ,DB的延长线交于N,RP,DC的延长线交于K,
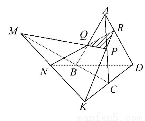
求证:M,N,K三点共线.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:选择题
已知向量a=(2,-3,5)与向量b=(3,λ,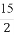 )平行,则λ=( )
)平行,则λ=( )
(A) (B)
(B) (C)-
(C)- (D)-
(D)-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1如图所示,以四边形ABB1A1为水平面,四边形BCC1B1的前面为正前方画出的三视图正确的是( )
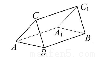

查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
一个正方体截去两个角后所得几何体的正视图(又称主视图)、侧视图(又称左视图)如图所示,则其俯视图为( )
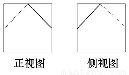
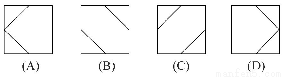
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:填空题
二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2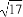 ,则该二面角的大小为 .
,则该二面角的大小为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:选择题
在三棱柱ABC-A1B1C1中,底面为边长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值为( )
(A)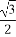 (B)
(B)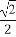 (C)
(C)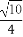 (D)
(D)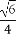
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为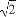 ,则此球的体积为( )
,则此球的体积为( )
(A)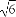 π (B)4
π (B)4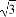 π (C)4
π (C)4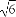 π (D)6
π (D)6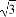 π
π
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:f(a·b)=af(b)+bf(a),f(2)=2,an=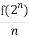 (n∈N*),bn=
(n∈N*),bn=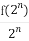 (n∈N*).
(n∈N*).
考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有( )
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com