
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:f(a·b)=af(b)+bf(a),f(2)=2,an=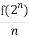 (n∈N*),bn=
(n∈N*),bn=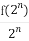 (n∈N*).
(n∈N*).
考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有( )
(A)1个 (B)2个 (C)3个 (D)4个
C
【解析】根据所给的四个条件,逐条验证即可.注意②中用特殊值验证,③④用定义判断.
∵f(0)=f(0×0)=0,
f(1)=f(1×1)=2f(1),
∴f(1)=0,①正确;
又f(1)=f((-1)×(-1))=-2f(-1),
∴f(-1)=0,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),
故f(x)不是偶函数,故②错;
∵f(2n)=f(2·2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,
∴ =
=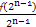 +1,
+1,
即bn=bn-1+1,
∴{bn}是等差数列,④正确;
b1=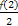 =1,
=1,
bn=1+(n-1)·1=n,
f(2n)=2nbn=n·2n,
an=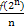 =2n,
=2n,
故数列{an}是等比数列,③正确.故选C.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:解答题
已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.
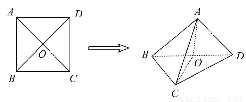
(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
设A,B,C,D是空间不共面的四个点,且满足 ·
· =0,
=0, ·
· =0,
=0, ·
· =0,则△BCD的形状是( )
=0,则△BCD的形状是( )
(A)钝角三角形 (B)直角三角形
(C)锐角三角形 (D)无法确定
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
用数学归纳法证明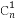 +
+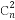 +…+
+…+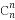 <
<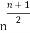 (n≥n0,n0∈N*),则n的最小值等于( )
(n≥n0,n0∈N*),则n的最小值等于( )
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)sin213°+cos217°-sin 13°cos 17°.
(2)sin215°+cos215°-sin 15°cos 15°.
(3)sin218°+cos212°-sin 18°cos 12°.
(4)sin2(-18°)+cos248°-sin(-18°)cos 48°.
(5)sin2(-25°)+cos255°-sin(-25°)cos 55°.
①试从上述五个式子中选择一个,求出这个常数.
②根据①的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
如果a<0,b<0,则必有( )
(A)a3+b3≥ab2+a2b (B)a3+b3≤ab2+a2b
(C)a3+b3>ab2+a2b (D)a3+b3<ab2+a2b
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:选择题
如图,虚线部分是四个象限的角平分线, 实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
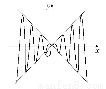
(A)x2sinx (B)xsinx
(C)x2cosx (D)xcosx
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:选择题
函数f(x)=x3+bx2+cx+d的大致图象如图所示,则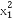 +
+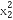 等于( )
等于( )
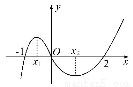
(A) (B)
(B)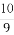 (C)
(C)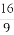 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:填空题
已知f(x)=x3-3x+m在区间[0,2]上任取三个不同的数a,b,c,均存在以f(a),f(b),f(c)为边长的三角形,则m的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com