
如图,虚线部分是四个象限的角平分线, 实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
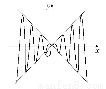
(A)x2sinx (B)xsinx
(C)x2cosx (D)xcosx
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:选择题
在三棱柱ABC-A1B1C1中,底面为边长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值为( )
(A)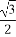 (B)
(B)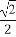 (C)
(C)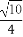 (D)
(D)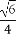
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:填空题
若数列{an}的通项公式an=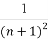 ,记cn=2(1-a1)·(1-a2)…(1-an),试通过计算c1,c2,c3的值,推测cn= .
,记cn=2(1-a1)·(1-a2)…(1-an),试通过计算c1,c2,c3的值,推测cn= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:f(a·b)=af(b)+bf(a),f(2)=2,an=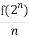 (n∈N*),bn=
(n∈N*),bn=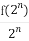 (n∈N*).
(n∈N*).
考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有( )
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ”的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ”中应用了( )
(A)分析法
(B)综合法
(C)分析法和综合法综合使用
(D)间接证法
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:填空题
已知函数f(x)=ex+2x,若f′(x)≥a恒成立,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:选择题
物体A以v=3t2+1(m/s)的速度在一直线l上运动,物体B在直线l上,且在物体A的正前方5m处,同时以v=10t(m/s)的速度与A同向运动,出发后物体A追上物体B所用的时间t(s)为( )
(A)3 (B)4 (C)5 (D)6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:解答题
已知某物体的温度θ(单位:摄氏度)随时间t(单位:分钟)的变化规律是:θ=m·2t+21-t(t≥0,且m>0).
(1)如果m=2,求经过多少时间,物体的温度为5摄氏度.
(2)若物体的温度总不低于2摄氏度,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com