
如图,在四面体ABCD中作截面PQR,若PQ,CB的延长线交于M,RQ,DB的延长线交于N,RP,DC的延长线交于K,
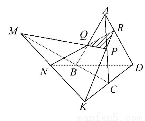
求证:M,N,K三点共线.
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(二)第一章第二节练习卷(解析版) 题型:选择题
设a,b∈R,则“a>1且0<b<1”是“a-b>0且 >1”的( )
>1”的( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(七)第二章第四节练习卷(解析版) 题型:选择题
已知函数f(x)=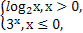 关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是( )
关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是( )
(A)a>1 (B)0<a<1
(C)a>2 (D)a<0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:选择题
已知集合A={x|y=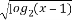 },B={y|y=
},B={y|y=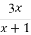 },则A∩B=( )
},则A∩B=( )
(A)[2,+∞) (B)[2,3)∪(3,+∞)
(C)(1,+∞) (D)[1,3)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:选择题
已知集合A={x|x≥0},B={0,1,2},则( )
(A)A⊆B (B)B⊆A
(C)A∪B=B (D)A∩B=?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:填空题
如图,在正方体ABCD-A1B1C1D1中,M,N分别是棱C1D1,C1C的中点.以下四个结论:

①直线AM与直线C1C相交;
②直线AM与直线BN平行;
③直线AM与直线DD1异面;
④直线BN与直线MB1异面.
其中正确结论的序号为 .(注:把你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:解答题
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC= .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.

(1)当平面ADB⊥平面ABC时,求CD.
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:解答题
如图,在圆锥PO中,已知PO= ,☉O的直径AB=2,C是
,☉O的直径AB=2,C是 的中点,D为AC的中点.
的中点,D为AC的中点.

求证:平面POD⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:解答题
已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.
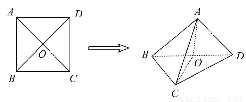
(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com