
如图,在圆锥PO中,已知PO= ,☉O的直径AB=2,C是
,☉O的直径AB=2,C是 的中点,D为AC的中点.
的中点,D为AC的中点.

求证:平面POD⊥平面PAC.
见解析
【解析】
【证明】如图,以O为坐标原点,OB,OC,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
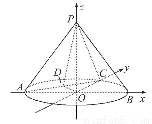
则O(0,0,0),A(-1,0,0),B(1,0,0),C(0,1,0),P(0,0,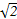 ),D(-
),D(-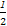 ,
,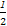 ,0).
,0).
设n1=(x1,y1,z1)是平面POD的一个法向量,则由n1·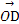 =0,n1·
=0,n1·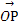 =0,
=0,
得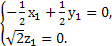
所以z1=0,x1=y1.取y1=1,得n1=(1,1,0).
设n2=(x2,y2,z2)是平面PAC的一个法向量,
则由n2·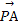 =0,
=0,
n2·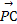 =0,得
=0,得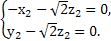
所以x2=-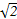 z2,y2=
z2,y2=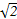 z2.
z2.
取z2=1,得n2=(-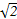 ,
,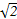 ,1).
,1).
因为n1·n2=(1,1,0)·(-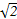 ,
,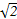 ,1)=0,
,1)=0,
所以n1⊥n2.
从而平面POD⊥平面PAC.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(三)第一章第三节练习卷(解析版) 题型:选择题
有关命题的说法错误的是( )
(A)命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”
(B)“x=1”是“x2-3x+2=0”的充分而不必要条件
(C)若p∧q为假命题,则p,q均为假命题
(D)对于命题p:?x∈R,使得x2+x+1<0.则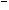 p:?x∈R,均有x2+x+1≥0
p:?x∈R,均有x2+x+1≥0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:解答题
如图,在四面体ABCD中作截面PQR,若PQ,CB的延长线交于M,RQ,DB的延长线交于N,RP,DC的延长线交于K,
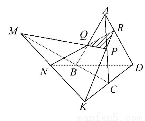
求证:M,N,K三点共线.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:解答题
在如图所示的几何体中,四边形ACC1A1是矩形,FC1∥BC,EF∥A1C1,∠BCC1=90°,点A,B,E,A1在一个平面内,AB=BC=CC1=2,AC=2 .
.

证明:(1)A1E∥AB.
(2)平面CC1FB⊥平面AA1EB.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
设α,β表示两个不同平面,l,m表示两条不同的直线,则下列命题正确的是( )
(A)若l⊥m,l?α,m?β,则α⊥β
(B)若l⊥α,m∥β,α⊥β,则l⊥m
(C)若l∥m,l?α,m⊥β,则α∥β
(D)若l⊥α,m⊥β,α∥β,则l∥m
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:选择题
已知 =(1,5,-2),
=(1,5,-2), =(3,1,z),若
=(3,1,z),若 ⊥
⊥ ,
, =(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )
=(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )
(A) ,-
,- ,4 (B)
,4 (B) ,-
,- ,4
,4
(C) ,-2,4 (D)4,
,-2,4 (D)4, ,-15
,-15
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:选择题
已知向量a=(2,-3,5)与向量b=(3,λ,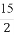 )平行,则λ=( )
)平行,则λ=( )
(A) (B)
(B) (C)-
(C)- (D)-
(D)-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1如图所示,以四边形ABB1A1为水平面,四边形BCC1B1的前面为正前方画出的三视图正确的是( )
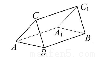

查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为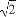 ,则此球的体积为( )
,则此球的体积为( )
(A)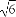 π (B)4
π (B)4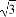 π (C)4
π (C)4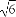 π (D)6
π (D)6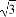 π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com