
°æƒø°ø“—÷™µ»±» ˝¡–{![]() }µƒ«∞nœÓ∫ÕŒ™
}µƒ«∞nœÓ∫ÕŒ™![]() £¨«“¬˙◊„2
£¨«“¬˙◊„2![]() £Ω
£Ω![]() £´m£®m° R£©£Æ
£´m£®m° R£©£Æ
£®¢Ò£©«Û ˝¡–{![]() }µƒÕ®œÓπ´ Ω£ª
}µƒÕ®œÓπ´ Ω£ª
£®¢Ú£©»Ù ˝¡–{![]() }¬˙◊„
}¬˙◊„![]() £¨«Û ˝¡–{
£¨«Û ˝¡–{![]() }µƒ«∞nœÓ∫Õ
}µƒ«∞nœÓ∫Õ![]() £Æ
£Æ
°æ¥∞∏°ø£®¢Ò£©![]() £®¢Ú£©
£®¢Ú£©![]()
°æΩ‚Œˆ°ø
(¢Ò)∑®“ª£∫”…«∞nœÓ∫ՔΠ˝¡–Õ®œÓπ´ Ωµƒπÿœµø…µ√ ˝¡–µƒÕ®œÓπ´ ΩŒ™![]() £ª
£ª
∑®∂˛£∫”…“‚ø…µ√ £¨‘Ú
£¨‘Ú![]() £¨æð¥Àø…µ√ ˝¡–µƒÕ®œÓπ´ ΩŒ™
£¨æð¥Àø…µ√ ˝¡–µƒÕ®œÓπ´ ΩŒ™![]() .
.
£®¢Ú£©”…£®¢Ò£©ø…µ√![]() £¨¡—œÓ«Û∫Õø…µ√
£¨¡—œÓ«Û∫Õø…µ√![]() .
.
(¢Ò)∑®“ª£∫
”…![]() µ√
µ√![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() £¨º¥
£¨º¥![]() £¨
£¨
”÷![]() £¨µ±
£¨µ±![]() ±∑˚∫œ…œ Ω£¨À˘“‘Õ®œÓπ´ ΩŒ™
±∑˚∫œ…œ Ω£¨À˘“‘Õ®œÓπ´ ΩŒ™![]() .
.
∑®∂˛£∫
”…![]() µ√
µ√
¥”∂¯”–![]() £¨
£¨
À˘“‘µ»±» ˝¡–π´±»![]() £¨ ◊œÓ
£¨ ◊œÓ![]() £¨“Ú¥ÀÕ®œÓπ´ ΩŒ™
£¨“Ú¥ÀÕ®œÓπ´ ΩŒ™![]() .
.
£®¢Ú£©”…£®¢Ò£©ø…µ√![]() £¨
£¨
![]() £¨
£¨
![]() .
.
°æµ„涰ø
±æÂ÷˜“™øº≤È ˝¡–«∞nœÓ∫Õ”ÎÕ®œÓπ´ Ωµƒπÿœµ£¨¡—œÓ«Û∫Õµƒ∑Ω∑®µ»÷™ ∂£¨“‚‘⁄øº≤È—ß…˙µƒ◊™ªØƒÐ¡¶∫Õº∆À„«ÛΩ‚ƒÐ¡¶.
°æ–հøΩ‚¥Ã‚
°æΩ· ¯°ø
18
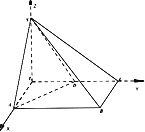
°æƒø°øÀƒ¿‚◊∂S£≠ABCDµƒµ◊√ÊABCDŒ™÷±Ω«Ã𖌣¨AB°ŒCD£¨AB°ÕBC£¨AB£Ω2BC£Ω2CD£Ω2£¨°˜SADŒ™’˝»˝Ω«–Œ£Æ
£®¢Ò£©µ„MŒ™¿‚AB…œ“ªµ„£¨»ÙBC°Œ∆Ω√ÊSDM£¨AM£Ω¶ÀAB£¨«Û µ ˝¶Àµƒ÷µ£ª
£®¢Ú£©»ÙBC°ÕSD£¨«Û∂˛√ÊΩ«A£≠SB£≠Cµƒ”ýœ“÷µ£Æ

°æ¥∞∏°ø£®¢Ò£©![]() £®¢Ú£©
£®¢Ú£©![]()
°æΩ‚Œˆ°ø
£®¢Ò£©”…œþ√Ê∆Ω––µƒ–‘÷ ∂®¿Ìø…µ√![]() £¨æð¥Àø…÷™Àƒ±þ–ŒBCDMŒ™∆Ω––Àƒ±þ–Œ£¨æð¥Àø…µ√
£¨æð¥Àø…÷™Àƒ±þ–ŒBCDMŒ™∆Ω––Àƒ±þ–Œ£¨æð¥Àø…µ√![]() .
.
£®¢Ú£©”…º∏∫Œπÿœµ£¨‘⁄∆Ω√Ê![]() ƒ⁄π˝µ„
ƒ⁄π˝µ„![]() ◊˜
◊˜![]() ÷±œþ
÷±œþ![]() ”⁄µ„
”⁄µ„![]() £¨“‘µ„EŒ™◊¯±Í‘≠µ„£¨EA∑ΩœÚŒ™X÷·£¨EC∑ΩœÚŒ™Y÷·£¨ES∑ΩœÚŒ™Z÷·Ω®¡¢ø’º‰◊¯±Íœµ£¨æð¥Àø…µ√∆Ω√Ê
£¨“‘µ„EŒ™◊¯±Í‘≠µ„£¨EA∑ΩœÚŒ™X÷·£¨EC∑ΩœÚŒ™Y÷·£¨ES∑ΩœÚŒ™Z÷·Ω®¡¢ø’º‰◊¯±Íœµ£¨æð¥Àø…µ√∆Ω√Ê![]() µƒ“ª∏ˆ∑®œÚ¡ø
µƒ“ª∏ˆ∑®œÚ¡ø![]() £¨∆Ω√Ê
£¨∆Ω√Ê![]() µƒ“ª∏ˆ∑®œÚ¡ø
µƒ“ª∏ˆ∑®œÚ¡ø![]() £¨æð¥Àº∆À„ø…µ√∂˛√ÊΩ«
£¨æð¥Àº∆À„ø…µ√∂˛√ÊΩ«![]() ”ýœ“÷µŒ™
”ýœ“÷µŒ™![]() .
.
£®¢Ò£©“ÚŒ™![]() ∆Ω√ÊSDM,
∆Ω√ÊSDM,![]()
![]() ∆Ω√ÊABCD,∆Ω√ÊSDM
∆Ω√ÊABCD,∆Ω√ÊSDM ![]() ∆Ω√ÊABCD=DM,À˘“‘
∆Ω√ÊABCD=DM,À˘“‘![]() £¨
£¨
“ÚŒ™![]() ,À˘“‘Àƒ±þ–ŒBCDMŒ™∆Ω––Àƒ±þ–Œ£¨”÷
,À˘“‘Àƒ±þ–ŒBCDMŒ™∆Ω––Àƒ±þ–Œ£¨”÷![]() ,À˘“‘MŒ™ABµƒ÷–µ„.
,À˘“‘MŒ™ABµƒ÷–µ„.
“ÚŒ™![]()
![]() .
.
£®¢Ú£©“ÚŒ™![]()
![]() £¨
£¨ ![]()
![]() £¨À˘“‘
£¨À˘“‘![]() ∆Ω√Ê
∆Ω√Ê![]() £¨”÷“ÚŒ™
£¨”÷“ÚŒ™![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨
À˘“‘∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £¨∆Ω√Ê
£¨∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨
‘⁄∆Ω√Ê![]() ƒ⁄π˝µ„
ƒ⁄π˝µ„![]() ◊˜
◊˜![]() ÷±œþ
÷±œþ![]() ”⁄µ„
”⁄µ„![]() £¨‘Ú
£¨‘Ú![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨“ÚŒ™
÷–£¨“ÚŒ™![]() £¨À˘“‘
£¨À˘“‘![]() £¨
£¨
”÷”…Â÷™![]() £¨À˘“‘
£¨À˘“‘![]() À˘“‘
À˘“‘![]() £¨
£¨
“‘œ¬Ω®œµ«ÛΩ‚.“‘µ„EŒ™◊¯±Í‘≠µ„£¨EA∑ΩœÚŒ™X÷·£¨EC∑ΩœÚŒ™Y÷·£¨ES∑ΩœÚŒ™Z÷·Ω®¡¢»ÁÕºÀ˘ æø’º‰◊¯±Íœµ£¨
‘Ú![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
…Ë∆Ω√Ê![]() µƒ∑®œÚ¡ø
µƒ∑®œÚ¡ø![]() £¨‘Ú
£¨‘Ú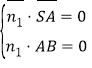 £¨À˘
£¨À˘![]() £¨
£¨
¡Ó![]() µ√
µ√![]() Œ™∆Ω√Ê
Œ™∆Ω√Ê![]() µƒ“ª∏ˆ∑®œÚ¡ø£¨
µƒ“ª∏ˆ∑®œÚ¡ø£¨
Õ¨¿Ìµ√![]() Œ™∆Ω√Ê
Œ™∆Ω√Ê![]() µƒ“ª∏ˆ∑®œÚ¡ø£¨
µƒ“ª∏ˆ∑®œÚ¡ø£¨
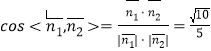 £¨“ÚŒ™∂˛√ÊΩ«
£¨“ÚŒ™∂˛√ÊΩ«![]() Œ™∂€Ω«.
Œ™∂€Ω«.
À˘“‘∂˛√ÊΩ«![]() ”ýœ“÷µŒ™
”ýœ“÷µŒ™![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() µƒÕºœÒ‘⁄
µƒÕºœÒ‘⁄![]() ¥¶µƒ«–œþ”Î÷±œþ
¥¶µƒ«–œþ”Î÷±œþ![]() ∆Ω––.
∆Ω––.
(1)«Û∫Ø ˝![]() µƒº´÷µ£ª
µƒº´÷µ£ª
(2)»Ù![]() £¨«Û µ ˝mµƒ»°÷µ∑∂Œß.
£¨«Û µ ˝mµƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°˜ABC÷–£¨ƒ⁄Ω«A£¨B£¨Cµƒ∂‘±þ∑÷±Œ™a£¨b£¨c«“√ʪ˝Œ™S£¨¬˙◊„S= ![]() bccosA
bccosA
£®1£©«ÛcosAµƒ÷µ£ª
£®2£©»Ùa+c=10£¨C=2A£¨«Ûbµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=2sin2x+2 ![]() sinxcosx
sinxcosx
£®¢Ò£©«Ûf£®x£©µƒ◊Ó–°’˝÷Ð∆⁄£ª
£®¢Ú£©«Û∫Ø ˝f£®x£©‘⁄«¯º‰ ![]() …œµƒ»°÷µ∑∂Œß£Æ
…œµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…ËxOy£¨![]() Œ™¡Ω∏ˆ∆Ω√Ê÷±Ω«◊¯±Íœµ£¨À¸√«æþ”–œýÕ¨µƒ‘≠µ„£¨Ox’˝∑ΩœÚµΩ
Œ™¡Ω∏ˆ∆Ω√Ê÷±Ω«◊¯±Íœµ£¨À¸√«æþ”–œýÕ¨µƒ‘≠µ„£¨Ox’˝∑ΩœÚµΩ![]() ’˝∑ΩœÚµƒΩ«∂»Œ™¶»£¨ƒ«√¥∂‘”⁄»Œ“‚µƒµ„M£¨‘⁄xOyœ¬µƒ◊¯±ÍŒ™£®x£¨y£©£¨ƒ«√¥À¸‘⁄
’˝∑ΩœÚµƒΩ«∂»Œ™¶»£¨ƒ«√¥∂‘”⁄»Œ“‚µƒµ„M£¨‘⁄xOyœ¬µƒ◊¯±ÍŒ™£®x£¨y£©£¨ƒ«√¥À¸‘⁄![]() ◊¯±Íœµœ¬µƒ◊¯±Í£®
◊¯±Íœµœ¬µƒ◊¯±Í£®![]() £¨
£¨![]() £©ø…“‘±Ì 挙£∫
£©ø…“‘±Ì 挙£∫![]() £Ωxcos¶»£´ysin¶»£¨
£Ωxcos¶»£´ysin¶»£¨![]() £Ωycos¶»£≠xsin¶»£Æ∏˘æð“‘…œ÷™ ∂«Ûµ√Õ÷‘≤3
£Ωycos¶»£≠xsin¶»£Æ∏˘æð“‘…œ÷™ ∂«Ûµ√Õ÷‘≤3![]() £≠
£≠![]() £´
£´![]() £≠1£Ω0µƒ¿Î–ƒ¬ Œ™
£≠1£Ω0µƒ¿Î–ƒ¬ Œ™
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™°˜ABC÷–£¨Ω«A°¢B°¢Cµƒ∂‘±þ∑÷±Œ™a°¢b°¢c£¨«“ ![]() =1£Æ
=1£Æ
£®1£©«ÛΩ«A£ª
£®2£©»Ùa=4 ![]() £¨«Ûb+cµƒ»°÷µ∑∂Œß£Æ
£¨«Ûb+cµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø Ææ≈¥Û÷≥ˆ£¨º”øÏÀÆŒ€»æ∑¿÷Œ£¨Ω®…Ë√¿¿ˆ÷–π˙.∏˘æðª∑±£≤ø√≈∂‘ƒ≥∫”¡˜µƒ√øƒÍŒ€ÀÆ≈≈∑≈¡ø![]() £®µ•Œª£∫∂÷£©µƒ¿˙ ∑Õ≥º∆ ˝æ𣨵√µΩ»Áœ¬∆µ¬ ∑÷≤º±Ì£∫
£®µ•Œª£∫∂÷£©µƒ¿˙ ∑Õ≥º∆ ˝æ𣨵√µΩ»Áœ¬∆µ¬ ∑÷≤º±Ì£∫

Ω´Œ€ÀÆ≈≈∑≈¡ø¬‰»Î∏˜◊ȵƒ∆µ¬ ◊˜Œ™∏≈¬ £¨≤¢ºŸ…Ë√øƒÍ∏√∫”¡˜µƒŒ€ÀÆ≈≈∑≈¡øœýª•∂¿¡¢.
£®1£©«Û‘⁄Œ¥¿¥3ƒÍ¿Ô£¨÷¡∂ý1ƒÍŒ€ÀÆ≈≈∑≈¡ø![]() µƒ∏≈¬ £ª£®2£©∏√∫”¡˜µƒŒ€ÀÆ≈≈∑≈∂‘—ÿ∫”µƒæ≠º√”∞œÏ»Áœ¬£∫µ±
µƒ∏≈¬ £ª£®2£©∏√∫”¡˜µƒŒ€ÀÆ≈≈∑≈∂‘—ÿ∫”µƒæ≠º√”∞œÏ»Áœ¬£∫µ±![]() ±£¨√ª”–”∞œÏ£ªµ±
±£¨√ª”–”∞œÏ£ªµ±![]() ±£¨æ≠º√À ߌ™10ÕÚ‘™£ªµ±
±£¨æ≠º√À ߌ™10ÕÚ‘™£ªµ±![]() ±£¨æ≠º√À ߌ™60ÕÚ‘™.Œ™ºı…ŸÀ ߣ¨œ÷”–»˝÷÷”¶∂‘∑Ω∞∏£∫
±£¨æ≠º√À ߌ™60ÕÚ‘™.Œ™ºı…ŸÀ ߣ¨œ÷”–»˝÷÷”¶∂‘∑Ω∞∏£∫
∑Ω∞∏“ª£∫∑¿÷Œ350∂÷µƒŒ€ÀÆ≈≈∑≈£¨√øƒÍ–Ë“™∑¿÷Œ∑—3.8ÕÚ‘™£ª
∑Ω∞∏∂˛£∫∑¿÷Œ310∂÷µƒŒ€ÀÆ≈≈∑≈£¨√øƒÍ–Ë“™∑¿÷Œ∑—2ÕÚ‘™£ª
∑Ω∞∏»˝£∫≤ª≤…»°¥Î ©.
‘±»Ωœ…œ ˆ»˝÷÷Œƒ∞∏£¨ƒƒ÷÷∑Ω∞∏∫√£¨≤¢«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() .
.
(1)≈–∂œ∫Ø ˝![]() µƒµ•µ˜–‘£ª
µƒµ•µ˜–‘£ª
(2)»Ù![]() ,µ±
,µ±![]() ±,≤ªµ» Ω
±,≤ªµ» Ω![]() ∫„≥…¡¢,«Û µ ˝
∫„≥…¡¢,«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=|2x©Å1|+|2x+a|£¨g£®x£©=x+3£Æ
£®1£©µ±a=2 ±£¨«Û≤ªµ» Ωf£®x£©£ºg£®x£©µƒΩ‚ºØ£ª
£®2£©…Ëa£æ ![]() £¨«“µ±x° [
£¨«“µ±x° [ ![]() £¨a] ±£¨f£®x£©°Ðg£®x£©£¨«Ûaµƒ»°÷µ∑∂Œß£Æ
£¨a] ±£¨f£®x£©°Ðg£®x£©£¨«Ûaµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com