
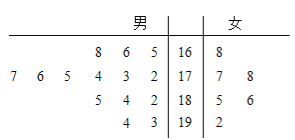
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(1)求男生成绩的中位数及女生成绩的平均值;
(2)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据中位数、平均数的概念写出中位数、平均数;(2)利用分层抽样及列举法、古典概型公式即可得出.
试题解析:
(1)男生有14人,中间两个成绩是175和176,它们的平均数为175.5,
因此男生的成绩的中位数为175.5,
女生的平均成绩![]() .
.
(2)用分层抽样的方法从“甲部门”和“乙部门”20人中抽取5人,每个人被抽到的概率是![]() .
.
根据茎叶图,“甲部门”人选有8人,“乙部门”人选有12人.
所以选中的“甲部门”人选有![]() 人,“乙部门”人选有
人,“乙部门”人选有![]() 人.
人.
记选中的“甲部门”的人员为![]() ,
,![]() ,选中的“乙部门”人员为
,选中的“乙部门”人员为![]() ,
,![]() ,
,![]() ,从这5人中选2人的所有可能情况为:
,从这5人中选2人的所有可能情况为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种,
共10种,
其中至少有1人是“甲部门”人选的结果有7种,
因此,至少有1人是“甲部门”人选的概率是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,点F为抛物线C1:![]() 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2:![]() 相切于点Q.
相切于点Q.

(Ⅰ)当直线PQ的方程为![]() 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数P变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为3的等差数列,数列{bn}是b1=1的等比数列,且![]() .
.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)令cn= an bn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ).
).
(Ⅰ) 当![]() 时,若
时,若![]() 在其定义域内为单调函数,求
在其定义域内为单调函数,求![]() 的取值范围;
的取值范围;
(Ⅱ) 当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立,如果存在,求
恒成立,如果存在,求![]() 的取值范围,如果不存在,说明理由(其中
的取值范围,如果不存在,说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() =2.71828…).
=2.71828…).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.![]() 是自然对数的底数.
是自然对数的底数.
(1)求曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)①若![]() 时,函数
时,函数![]() 既有极大值又有极小值,求实数
既有极大值又有极小值,求实数![]() 的取值范围;
的取值范围;
②若![]() ,
,![]() ,若
,若![]() 对一切正实数
对一切正实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com