
���� ��1����f�䣨x��=ex-a��f'��0��=0����a=1���Ӷ�f�䣨x��=ex-1���ɴ����õ����������������f��x���ĵ������䣮
��2����$\frac{g��{x}_{2}��-g��{x}_{1}��}{{x}_{2}-{x}_{1}}$��m����x1��x2�����εã�g��x2��-mx2��g��x1��-mx1�����F��x��=g��x��-mx����F��x����R�ϵ����������Ӷ�m��g�䣨x����R�Ϻ�������ɴ������ʵ��m��ȡֵ��Χ��
��3��ex��x+1��ȡ$x=-\frac{i}{2n}$��i=1��3������2n-1����${��\frac{2n-i}{2n}��^n}��{e^{-\frac{i}{2}}}$���ɴ������ۼӷ���֤��${1^n}+{3^n}+��+{��2n-1��^n}��\frac{{\sqrt{e}}}{1-e}{��2n��^n}$��
��� �⣺��1����f��x��=ex-a��x+1����
��f�䣨x��=ex-a��
��f�䣨0��=1-a=0��
��a=1����f�䣨x��=ex-1��
��f�䣨x��=ex-1��0����x��0����f�䣨x��=ex-1��0����x��0��
�ຯ��f��x���ĵ���������Ϊ��0��+�ޣ�������������Ϊ��-�ޣ�0��������6�֣�
��2����$\frac{g��{x}_{2}��-g��{x}_{1}��}{{x}_{2}-{x}_{1}}$��m����x1��x2�����εã�g��x2��-mx2��g��x1��-mx1��
���F��x��=g��x��-mx����F��x����R�ϵ���������
��F�䣨x��=g�䣨x��-m��0����m��g�䣨x����R�Ϻ������
$g'��x��={e^x}-a-\frac{a}{e^x}��2\sqrt{{e^x}•��-\frac{a}{e^x}��}-a=-a+2\sqrt{-a}={��\sqrt{-a}+1��^2}-1��3$��
��m��3��
��ʵ��m��ȡֵ��Χ�ǣ�-�ޣ�3]��
֤������3���ɣ�1��֪ex��x+1��
ȡ$x=-\frac{i}{2n}$��i=1��3������2n-1���ã�$1-\frac{i}{2n}��{e^{-\frac{i}{2n}}}$��
��${��\frac{2n-i}{2n}��^n}��{e^{-\frac{i}{2}}}$��
�ۼӵã�${��\frac{1}{2n}��^n}+{��\frac{3}{2n}��^n}+��+{��\frac{2n-1}{2n}��^n}��{e^{-\frac{2n-1}{2}}}+{e^{-\frac{2n-3}{2}}}+��+{e^{-\frac{1}{2}}}=\frac{{{e^{-\frac{1}{2}}}��1-{e^{-n}}��}}{{1-{e^{-1}}}}��\frac{{\sqrt{e}}}{1-e}$��
��${1^n}+{3^n}+��+{��2n-1��^n}��\frac{{\sqrt{e}}}{1-e}{��2n��^n}$������14�֣�
���� ���⿼��ʵ��ֵ�������麯���ĵ����Ե����ۣ�����ʵ��ֵ�������鲻��ʽ��֤�������е��⣬����ʱҪ�������⣬ע������ʺ��ۼӷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | $-\frac{3}{4}$ | C�� | $\frac{3}{4}i$ | D�� | $-\frac{3}{4}i$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
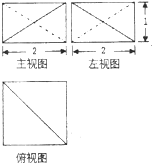
| A�� | 4 | B�� | $\frac{4}{3}$ | C�� | 2 | D�� | $\frac{8}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x��M����x∉N | |
| B�� | ��x��N����x��M | |
| C�� | ����x1��M��x1��N���ִ���x2��M��x2∉N | |
| D�� | ����x0��M��x0∉N |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com