
分析 (1)两圆方程相减,可得公共弦所在直线的方程;
(2)求出圆心到公共弦所在直线的距离,利用勾股定理求公共弦的长.
解答 解:(1)两圆方程相减,可得公共弦所在直线的方程x-2y+4=0;
(2)圆${C_1}:{x^2}+{y^2}-2x+10y-24=0$的圆心坐标为(1,-5),半径为5$\sqrt{2}$,
圆心到公共弦所在直线的距离d=$\frac{|1+10+4|}{\sqrt{1+4}}$=3$\sqrt{5}$,
∴公共弦的长=2$\sqrt{50-45}$=2$\sqrt{15}$.
点评 本题考查圆与圆的位置关系,考查点到直线距离公式的运用,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
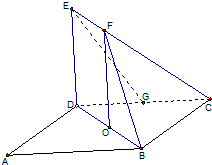 如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.
如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com