Question

14．已知函数$f（x）=lnx+\frac{1}{2}a{x^2}-（{a+1}）x（{a∈R}）$．
（I）a=1时，求函数y=f（x）的零点个数；
（Ⅱ）当a＞0时，若函数y=f（x）在区间[1，e]上的最小值为-2，求a的值；
（Ⅲ）若关于x的方程$f（x）=\frac{1}{2}a{x^2}$有两个不同实根x₁，x₂，求实数a的取值范围并证明：${x_1}•{x_2}＞{e^2}$．

Answer 1

分析 （I）a=1时，确定函数y=f（x）在（0，+∞）上单调递增，利用$f（1）=-\frac{3}{2}＜0，f（4）=ln4＞0$，即可求函数y=f（x）的零点个数；
（Ⅱ）当a＞0时，分类讨论，确定函数的单调性，利用函数y=f（x）在区间[1，e]上的最小值为-2，求a的值；
（Ⅲ）因为方程$f（x）=\frac{1}{2}a{x^2}$有两个不同实根x₁，x₂，即lnx-（a+1）x=0有两个不同实根x₁，x₂，得$a+1=\frac{lnx}{x}$，构造函数，由此即可证明结论．

解答 解：（ I）当a=1时$f（x）=lnx+\frac{1}{2}{x^2}-2x，f'（x）=\frac{1}{x}+x-2=\frac{{{{（{x-1}）}^2}}}{x}≥0$．
所以函数y=f（x）在（0，+∞）上单调递增；…（2分）
又因为$f（1）=-\frac{3}{2}＜0，f（4）=ln4＞0$．所以函数y=f（x）有且只有一个零点…（3分）
（ II）函数$f（x）=lnx+\frac{1}{2}a{x^2}-（a+1）x$的定义域是（0，+∞）．
当a＞0时，$f'（x）=\frac{1}{x}+ax-（a+1）=\frac{{a{x^2}-（a+1）x+1}}{x}（x＞0）$令f'（x）=0，即$f'（x）=\frac{{a{x^2}-（a+1）x+1}}{x}=\frac{（x-1）（ax-1）}{x}=0$，
所以x=1或$x=\frac{1}{a}$．…（4分）
当$0＜\frac{1}{a}≤1$，即a≥1时，f（x）在[1，e]上单调递增，
所以f（x）在[1，e]上的最小值是$f（1）=-\frac{1}{2}a-1=-2$，解得a=2；…（5分）
当$1＜\frac{1}{a}＜e$，即$\frac{1}{e}＜a＜1$时，f（x）在[1，e]上的最小值是$f（\frac{1}{a}）=-lna-\frac{1}{2a}-1=-2$，即$lna+\frac{1}{2a}=1$．
令$h（a）=lna+\frac{1}{2a}$，h′（a）=$\frac{2a-1}{2{a}^{2}}$=0，可得$a=\frac{1}{2}$，
∴h（a）在$（{\frac{1}{e}，\frac{1}{2}}）$单调递减，在$（{\frac{1}{2}，1}）$单调递增；
而$h（\frac{1}{e}）=-1+\frac{e}{2}＜1$，$h（1）=\frac{1}{2}＜1$，不合题意； …（7分）
当$\frac{1}{a}≥e$ 即$0＜a≤\frac{1}{e}$时，f（x）在[1，e]上单调递减，
所以f（x）在[1，e]上的最小值是$f（e）=1+\frac{1}{2}a{e^2}-（a+1）e=-2$，解得$a=\frac{6-2e}{{2e-{e^2}}}＜0$，
不合题意    综上可得a=2． …（8分）
（ III） 因为方程$f（x）=\frac{1}{2}a{x^2}$有两个不同实根x₁，x₂，即lnx-（a+1）x=0有两个不同实根x₁，x₂，
得$a+1=\frac{lnx}{x}$，
令$φ（x）=\frac{lnx}{x}，{φ^'}（x）=\frac{1-lnx}{x^2}$，
∴$φ（x）=\frac{lnx}{x}$在（0，e）上单调递增，（e，+∞）上单调递减，
∴x=e时，∴$φ（x）=\frac{lnx}{x}$取得最大值$\frac{1}{e}$，…（9分）
由φ（1）=0，得当x∈（0，1）时，φ（x）＜0，而当x∈（1，+∞），φ（x）＞0，φ（x）图象如下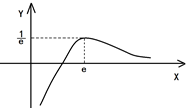

∴$a+1∈（{0，\frac{1}{e}}）$ 即当$-1＜a＜\frac{1}{e}-1$时$f（x）=\frac{1}{2}a{x^2}$有两个不同实根x₁，x₂…（10分）
满足lnx₁=（a+1）x₁，lnx₂=（a+1）x₂两式相加得：lnx₁x₂=（a+1）（x₁+x₂），两式相减得$ln\frac{x_2}{x_1}=（{a+1}）（{{x_2}-{x_1}}）$，
∴$\frac{{ln{x_1}{x_2}}}{{ln\frac{x_2}{x_1}}}=\frac{{{x_1}+{x_2}}}{{{x_2}-{x_1}}}$．
不妨设x₁＜x₂，要证${x_1}•{x_2}＞{e^2}$，只需证$ln{x_1}{x_2}=\frac{{{x_1}+{x_2}}}{{{x_2}-{x_1}}}•ln\frac{x_2}{x_1}＞2$，
即证$ln\frac{x_2}{x_1}＞\frac{{2（{{x_2}-{x_1}}）}}{{{x_1}+{x_2}}}=\frac{{2（{\frac{x_2}{x_1}-1}）}}{{1+\frac{x_2}{x_1}}}$，
设$t=\frac{x_2}{x_1}（{t＞1}）$，令$F（t）=lnt-\frac{{2（{t-1}）}}{1+t}=lnt+\frac{4}{t+1}-2$，…（12分）
则${F^'}（t）=\frac{1}{t}-\frac{4}{{{{（{t+1}）}^2}}}=\frac{{{{（{t-1}）}^2}}}{{t{{（{t-1}）}^2}}}＞0$，∴函数F（t）在（1，+∞）上单调递增，而F（1）=0．
∴F（t）＞0，即$lnt＞\frac{{2（{t-1}）}}{1+t}$．∴${x_1}•{x_2}＞{e^2}$．…（14分）

点评 本题考查导数知识的综合运用，考查函数的单调性与最值，考查函数的零点，考查不等式的证明，考查学生分析解决问题的能力，难度大．