
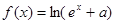 (
(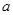 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数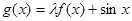 是区间[-1,1]上的减函数
是区间[-1,1]上的减函数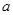 的值;
的值;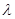 的取值范围;
的取值范围; 在
在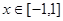 上恒成立,求
上恒成立,求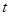 的取值范围。
的取值范围。科目:高中数学 来源:不详 题型:解答题
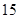 元,销售价是
元,销售价是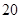 元,月平均销售
元,月平均销售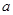 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为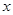
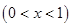 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为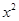 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是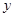 (元).
(元).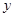 与
与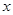 的函数关系式;
的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
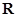 ,其导函数f'(x)的图象如图所示,则对于任意
,其导函数f'(x)的图象如图所示,则对于任意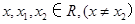 ,下列结论正确的是( )
,下列结论正确的是( )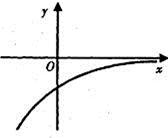
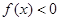 恒成立;
恒成立;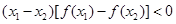 ;
;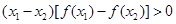 ;
;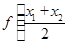 >
> 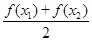 ;
;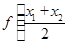 <
< 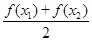 .
.| A.①③ | B.①③④ | C.②④ | D.②⑤ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
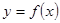 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
(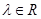 )
)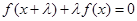 对任意实数
对任意实数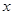 都成立,则称
都成立,则称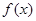 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有 —伴随函数”的结论:
—伴随函数”的结论: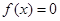 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;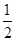 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;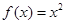 是一个“
是一个“ —伴随函数”;
—伴随函数”;| A.1个; | B.2个; | C.3个; | D.0个; |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com