
分析 (I)利用递推式可得an+an-1=2或an-an-1=2,通过分类讨论即可得出;
(II)利用“裂项求和”即可得出.
解答 解:(I)∵an>0,${S_n}=\frac{1}{4}({a_n}^2+4n-1)$,
∴当n=1时,a1=$\frac{1}{4}({a}_{1}^{2}+4-1)$,解得a1=1或3.
当n≥2时,an=Sn-Sn-1=$\frac{1}{4}({a}_{n}^{2}+4n-1)$-$\frac{1}{4}({a}_{n-1}^{2}+4n-5)$,
化为(an+an-1-2)(an-an-1-2)=0,
∴an+an-1=2或an-an-1=2,
①若an+an-1=2,当a1=1时,可得an=1,(n∈N*),数列{an}为常数数列,舍去;当a1=3时,可得a2=-1,与an>0矛盾,舍去;
②若an-an-1=2,当a1=1时,可得an=2n-1,(n∈N*),满足题意.当a1=3时,可得an=2n+1,(n∈N*),满足题意.
综上可得:an=2n±1,(n∈N*).
(II)当an=2n-1,${b_n}=\frac{2}{{{a_n}•{a_{n-1}}}}$=$\frac{2}{(2n-1)(2n-3)}$=$\frac{1}{2n-3}-\frac{1}{2n-1}$,
则数列{bn}的前项n和Tn=$(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-3}-\frac{1}{2n-1})$=1-$\frac{1}{2n-1}$=$\frac{2n-2}{2n-1}$.
同理可得:当an=2n+1,${b_n}=\frac{2}{{{a_n}•{a_{n-1}}}}$=$\frac{1}{2n-1}-\frac{1}{2n+1}$,则数列{bn}的前项n和Tn=1-$\frac{1}{2n+1}$=$\frac{2n}{2n+1}$.
点评 本题考查了递推式的应用、等差数列的通项公式、分类讨论方法、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
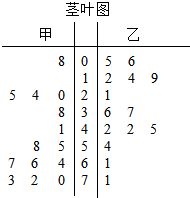 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )| A. | 55,36 | B. | 55.5,36.5 | C. | 56.5,36.5 | D. | 58,37 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{lg2}{2},\frac{lge}{e}})$ | B. | $({0,\frac{1}{e}})$ | C. | $({\frac{lg2}{2},e})$ | D. | $({0,\frac{lg2}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com