分析:解法一:在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中,也可以建立空间直角坐标系,设定参量求解.这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.设AB=a,则A
1(0,0,2a),C(0,a,0),C
1(0,a,2a),D(a,0,a)
(Ⅰ)
=(a,-a,-a),
=(0,a,-2a)
(Ⅱ)又∵
=(a,0,-a),
=(0,a,0),∴
⊥
,
⊥
,∴A
1D⊥平面ACD
解法二:
(Ⅰ)求异面直线所成的角,可用几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.连接AC
1交A
1C于点E,取AD中点F,连接EF,则EF∥C
1D,∴直线EF与A
1C所成的角就是异面直线C
1D与A
1C所成的角.
(Ⅱ)欲证平面A
1DC⊥平面ADC,先证直线与平面垂直,由题意可得:AC⊥A
1D,AD⊥A
1D,∴A
1D⊥平面ACD,又A
1D?平面A
1CD,∴平面A
1DC⊥平面ADC
解答:解:解法一:(Ⅰ)建立如图所示的空间直角坐标系设AB=a,
则A
1(0,0,2a),C(0,a,0),C
1(0,a,2a),D(a,0,a)(2分)
于是
=(a,-a,-a),
=(0,a,-2a)
∵cos<
,
>=
=
=
,(6分)
∴异面直线C
1D与A
1C所成的角为arccos
(7分)
(Ⅱ)∵
=(a,0,-a),
=(0,a,0),
∴
•
=a
2+0-a
2=0,
•
=0(10分)
则
⊥
,
⊥
∴A
1D⊥平面ACD(12分)
又A
1D?平面A
1CD,
∴平面A
1DC⊥平面ADC(14分)
解法二:
(Ⅰ)连接AC
1交A
1C于点E,取AD中点F,连接EF,则EF∥C
1D
∴直线EF与A
1C所成的角就是异面直线C
1D与A
1C所成的角(2分)
设AB=a,
则C
1D=
=
a,
A
1C=
=
a,AD=
=
a.
△CEF中,CE=
A
1C=
a,EF=
C
1D=
a,
直三棱柱中,∠BAC=90°,则AD⊥AC(4分)
CF=
=
=
a(4分)
∵cos∠CEF=
=
=
,(6分)
∴异面直线C
1D与A
1C所成的角为arccos
(7分)
(Ⅱ)直三棱柱中,∠BAC=90°,∴AC⊥平面ABB
1A
1,则AC⊥A
1D(9分)
又AD=
a,A
1D=
a,AA
1=2a,
则AD
2+A
1D
2=AA
12,于是AD⊥A
1D(12分)
∴A
1D⊥平面ACD又A
1D?平面A
1CD,
∴平面A
1DC⊥平面ADC(14分)
点评:本小题主要考查空间线面关系、面面关系、二面角的度量,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

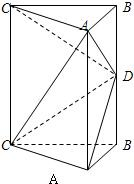 如图,直三棱柱ABC-A1B1C1中,AB=AC=
如图,直三棱柱ABC-A1B1C1中,AB=AC=

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB= 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.