
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1) 若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2) 若a∈[2,4],b∈[0,6],求方程没有实根的概率.
解:设“方程有两个正根”的事件为A,“方程没有实根”的事件为B.
(1) 由题意知本题是一个古典概型,用(a,b)表示一枚骰子掷两次所得到的点数.依题意知,基本事件(a,b)的总数有36个,二次方程x2-2(a-2)x-b2+16=0有两正根,等价于
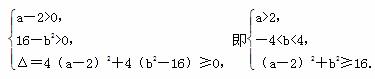 则事件A包含的基本事件为(6,1)、(6,2)、(6,3)、(5,3)共4个.
则事件A包含的基本事件为(6,1)、(6,2)、(6,3)、(5,3)共4个.
∴所求的概率为P(A)=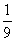 .
.
(2) 由题意知本题是一个几何概型,试验的全部结果构成区域Ω={(a,b)|2≤a≤4,0≤b≤6}, 其面积为S(Ω)=12.满足条件的事件为:B={(a,b)|2≤a≤4,0≤b≤6,(a-2)2+b2<16},其面积为S(B)=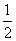 ×
×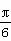 ×4×4+
×4×4+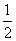 ×2×
×2×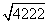 =
=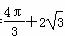
∴ 所求的概率P(B)=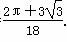 .
.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为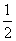 ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
(1) 求这批产品通过检验的概率;
(2) 已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
在人民商场付款处排队等候付款的人数及其概率如下:
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
则至少有两人排队的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
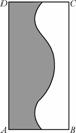
如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1 000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
下表中有三个游戏规则,袋子中分别装有大小相同的球,从袋子中取球,分别计算甲获胜的概率,说明哪个游戏是公平的?
| 游戏1 | 游戏2 | 游戏3 |
| 1个红球和1个白球 | 2个红球和2个白球 | 3个红球和1个白球 |
| 取1个球 | 取1个球,再取1个球 | 取1个球,再取1个球 |
| 取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
| 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
分析:游戏是否公平的关键是看甲、乙获胜的概率是否相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
某中学高中一年级有400人,高中二年级有320人,高中三年级有280人,现从中抽取一个容量为200人的样本,则高中二年级被抽取的人数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com