
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为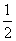 ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
(1) 求这批产品通过检验的概率;
(2) 已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同.
(1) 求3个学生选择了3门不同的选修课的概率;
(2) 求恰有2门选修课这3个学生都没有选择的概率;
(3) 设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.4.用击中环数的期望与方差比较两名射手的射击水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列六个命题:
① 两个向量相等,则它们的起点相同,终点相同;
② 若|a|=|b|,则a=b;
③ 若 ,则A、B、C、D四点构成平行四边形;
,则A、B、C、D四点构成平行四边形;
④ 在ABCD中,一定有 ;
;
⑤ 若m=n,n=p,则m=p;
⑥ 若a∥b,b∥c,则a∥c.
其中错误的命题有________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,△ABC中,在AC上取一点N,使AN= AC;在AB上取一点M,使得AM=
AC;在AB上取一点M,使得AM= AB;在BN的延长线上取点P,使得NP=
AB;在BN的延长线上取点P,使得NP=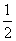 BN;在CM的延长线上取点Q,使得
BN;在CM的延长线上取点Q,使得 =λ
=λ 时,
时, =
= ,试确定λ的值.
,试确定λ的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1) 若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2) 若a∈[2,4],b∈[0,6],求方程没有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com