
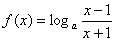 (其中
(其中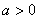 且
且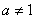 ),
),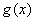 是
是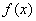 的反函数.
的反函数.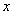 的方程
的方程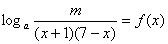 在区间
在区间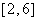 上有实数解,求实数
上有实数解,求实数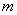 的取值范围;
的取值范围;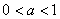 时,讨论函数
时,讨论函数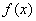 的奇偶性和增减性;
的奇偶性和增减性;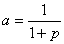 ,其中
,其中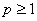 .记
.记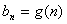 ,数列
,数列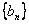 的前
的前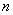 项的和为
项的和为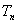 (
(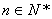 ),
),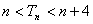 .
.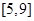 ;(2)奇函数,减函数;(3)证明见解析.
;(2)奇函数,减函数;(3)证明见解析.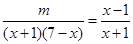 ,从而有
,从而有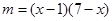 ,方程在
,方程在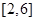 上有解,就变为求函数
上有解,就变为求函数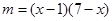 在
在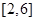 上的值域,转化时注意对数的真数为正;(2)奇偶性和单调性我们都根据定义加以解决;(3)
上的值域,转化时注意对数的真数为正;(2)奇偶性和单调性我们都根据定义加以解决;(3) ,
,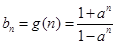
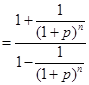
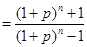 ,要证明不等式成立,最好是能把和
,要证明不等式成立,最好是能把和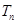 求出来,但看其通项公式
求出来,但看其通项公式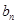 ,这个和是不可能求出的,由于我们只要证明不等式
,这个和是不可能求出的,由于我们只要证明不等式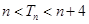 ,那么我们能不能把
,那么我们能不能把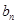 放缩后可求和呢?
放缩后可求和呢?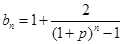 ,显然
,显然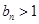 ,即
,即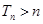 ,左边易证,又由二项式定理
,左边易证,又由二项式定理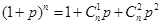
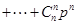 ,在
,在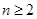 时,
时,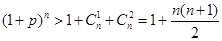 ,所以
,所以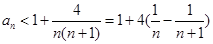 ,注意到
,注意到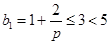 ,至此不等式的右边可以求和了,
,至此不等式的右边可以求和了,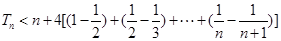
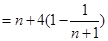
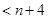 ,得证.
,得证.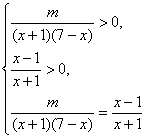 转化为求函数
转化为求函数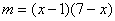 在
在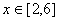 上的值域,
上的值域,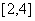 上递增、在
上递增、在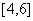 上递减,所以
上递减,所以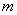 的最小值5,最大值9。所以
的最小值5,最大值9。所以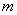 的取值范围为
的取值范围为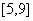 。 4分
。 4分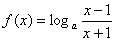 的定义域为
的定义域为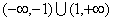 , 5分
, 5分 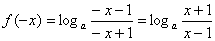 ,
, 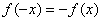 ,所以函数
,所以函数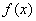 为奇函数。 6分
为奇函数。 6分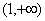 上函数的增减性.
上函数的增减性.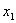 、
、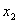
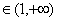 ,设
,设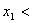
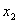 ,令
,令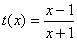 ,则
,则 ,
,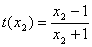 ,所以
,所以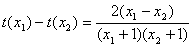
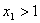 ,
, ,
,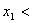
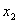 ,所以
,所以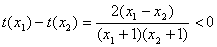 . 7分
. 7分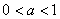 时,
时,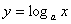 是减函数,所以
是减函数,所以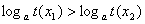 .由定义知在
.由定义知在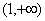 上函数是减函数. 8分
上函数是减函数. 8分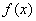 是奇函数,所以在
是奇函数,所以在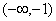 上函数也是减函数. 9分
上函数也是减函数. 9分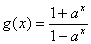 ; 10分
; 10分 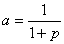 ,
,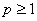 ,所以
,所以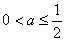 ,
,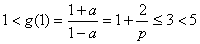 。 11分
。 11分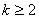 ,
,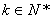 时,则
时,则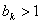 , 12分
, 12分 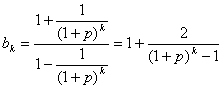 , 13分
, 13分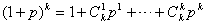 , 14分
, 14分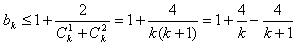 ,
,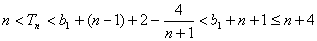 。 18分
。 18分 

科目:高中数学 来源:不详 题型:填空题
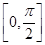 上单调递增,在区间
上单调递增,在区间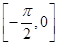 上单调递减.其中是真命题的是________.(写出所有真命题的序号)
上单调递减.其中是真命题的是________.(写出所有真命题的序号)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
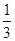 x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是( )
x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是( )A. | B.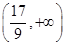 |
| C.(-∞,2] | D.(-∞,2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
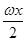 +2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
+2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
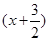 =-f(x),且函数y=f
=-f(x),且函数y=f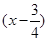 为奇函数,给出以下四个命题:
为奇函数,给出以下四个命题: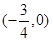 对称;
对称;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
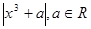 在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-
在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-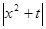 有4个零点,则实数t的取值范围为( )
有4个零点,则实数t的取值范围为( )A.(1,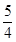 ) ) | B.(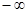 1,-1) 1,-1) |
C.(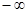 1,-1) 1,-1)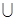 (1, (1, 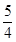 ) ) | D.(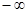 1,-1) 1,-1)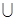 (1,2) (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com