
分析 (1)令f(x)=1解出A点坐标,利用AB=2得出B点坐标,把B点坐标代入g(x)解出a;
(2)利用对数的运算性质去掉对数符号列出方程解出x,结合函数的定义域得出x的值.
解答 解:(1)解log2(x+2)=1得x=0,∴A(0,1),
∵AB=2,∴B(2,1).
把B(2,1)代入g(x)得loga2=1,∴a=2.
(2)∵f(x)+g(x)=3,
∴log2(x+2)+log2x=log2[x(x+2)]=3,
∴x(x+2)=8,解得x=-4或x=2.
由函数有意义得$\left\{\begin{array}{l}{x>0}\\{x+2>0}\end{array}\right.$,解得x>0.
∴方程f(x)+g(x)=3的解为x=2.
点评 本题考查了对数函数的图象与性质,对数方程的解法,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:解答题
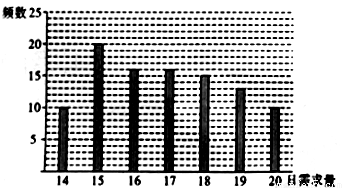
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.
(1)若蛋糕店一天制作17个生日蛋糕,
①求当天的利润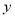 (单位:元)关于当天需求量
(单位:元)关于当天需求量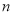 (单位:个,
(单位:个,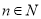 )的函数解析式;
)的函数解析式;
②在当天的利润不低于750元的条件下,求当天需求量不低于18个的概率.
(2)若蛋糕店计划一天制作16个或17个生日蛋糕,请你以蛋糕店一天利润的期望值为决定依据,判断应该制作16个是17个?
查看答案和解析>>
科目:高中数学 来源:2017届湖南石门县一中高三9月月考数学(文)试卷(解析版) 题型:解答题
已知函数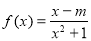 是奇函数,
是奇函数, 是偶函数.
是偶函数.
(1)求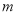 ,
,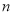 的值;
的值;
(2)不等式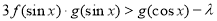 对任意
对任意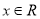 恒成立,求实数
恒成立,求实数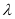 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届湖南石门县一中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知命题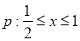 ,命题
,命题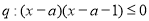 ,若
,若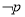 是
是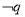 的必要不充分条件,则实数
的必要不充分条件,则实数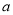 的取值范围是( )
的取值范围是( )
A.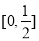 B.
B.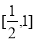
C.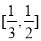 D.
D.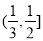
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9x±4y=0 | B. | 4x±9y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{MC}+\overrightarrow{MB}=\overrightarrow 0$ | B. | $\overrightarrow{MC}+\overrightarrow{AB}=\overrightarrow 0$ | C. | $\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow 0$ | D. | $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow 0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com