
| A. | 0<f'(2)<f'(3)<f(3)-f(2) | B. | 0<f'(2)<f(3)-f(2)<f'(3) | C. | 0<f'(3)<f(3)-f(2)<f'(2) | D. | 0<f(3)-f(2)<f'(2)-f'(3) |
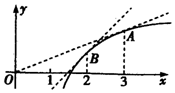
分析 由题意已知函数f(x)的图象,先判断它的单调性,然后根据函数图象斜率的变化,判断f(x)′的增减性,最后根据函数的凸凹性进行判断,从而求解.
解答 解:由函数f(x)的图象可知:
当x≥0时,f(x)单调递增,且当x=0时,f(0)<0,
∴f′(2),f′(3),f(3)-f(2)>0,
由此可知f′(x)>0,
∵直线的斜率逐渐减小,
∴f′(x)单调递减,
∴f′(2)>f′(3),
∵f(x)为凸函数,
∴f(3)-f(2)<f′(2)
∴0<f′(3)<f(3)-f(2)<f′(2),
故选C.
点评 此题主要考查函数导数与函数单调性之间的关系,掌握并会熟练运用导数与函数单调性的关系,另外还考查学生的读图能力,要善于从图中获取信息.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级 | 高一 | 高二 | 高三 |
| 数量 | 50 | 150 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150 | B. | 200 | C. | 500 | D. | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
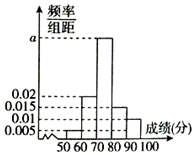 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.| 男生 | 女生 | 合计 | |
| 优 秀 | |||
| 不优秀 | |||
| 合 计 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com