
【题目】已知点![]() 在离心率为
在离心率为![]() 的椭圆
的椭圆![]() 上,则该椭圆的内接八边形面积的最大值为_____.
上,则该椭圆的内接八边形面积的最大值为_____.
【答案】![]()
【解析】
先由点![]() 在离心率为
在离心率为![]() 的椭圆
的椭圆![]() ,可求出
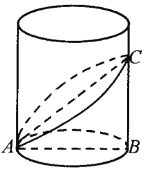
,可求出![]() ,由于椭圆可以看做是用一个不平行底面的圆去截圆柱所得的图形,且椭圆在底面的摄影是底面圆,由射影的性质可知
,由于椭圆可以看做是用一个不平行底面的圆去截圆柱所得的图形,且椭圆在底面的摄影是底面圆,由射影的性质可知![]() ,即
,即![]() ,且椭圆内接八边形的射影为底面圆上的内接八边形,又由平面几何知识易知圆内接八边形中内接正八边形面积最大,求出最大值,然后可得答案.
,且椭圆内接八边形的射影为底面圆上的内接八边形,又由平面几何知识易知圆内接八边形中内接正八边形面积最大,求出最大值,然后可得答案.
解:由点![]() 在椭圆
在椭圆![]() ,得
,得![]() ,
,
又因为![]() ,
,![]() ,得
,得![]() ,
,![]()
由于椭圆可以看做是用一个不平行底面的圆去截圆柱所得的图形,如图所示
且椭圆在底面的摄影是底面圆,其中![]() ,
,![]()
由射影的性质可知![]() ,
,![]() 为两平面的二面角的平面角
为两平面的二面角的平面角
记椭圆内接八边形面积为![]() ,对应的在底面圆上的射影也是八边形,面积为
,对应的在底面圆上的射影也是八边形,面积为![]()
所以![]() ,即
,即![]() ,
,
其中![]() ,
,![]() ,底面圆半径
,底面圆半径![]()
由平面几何知识易知圆内接八边形中内接正八边形面积最大为![]()
所以椭圆内接八边形面积最大为![]()


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】(1)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
概率 |
|
|
|
|
|
|
求至少3人排队等候的概率是多少?
(2)在区间![]() 上随机取两个数m,n,求关于x的一元二次方程
上随机取两个数m,n,求关于x的一元二次方程![]() 有实根的概率.
有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
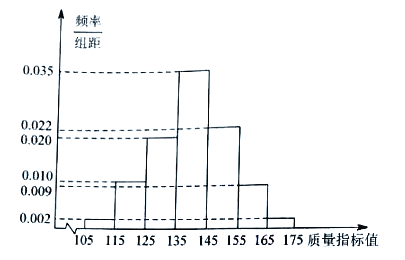
(1)求这1000件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表)
(同一组数据用该区间的中点值作代表)
(2)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中以
,其中以![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ⅱ)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求
表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.先把高二年级的![]() 名学生编号:
名学生编号:![]() 到
到![]() ,再从编号为
,再从编号为![]() 到
到![]() 的学生中随机抽取
的学生中随机抽取![]() 名学生,其编号为
名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() 的学生,这种抽样方法是分层抽样法
的学生,这种抽样方法是分层抽样法
B.线性回归直线![]() 不一定过样本中心
不一定过样本中心![]()
C.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于
的值越接近于![]()
D.若一组数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数是
的平均数是![]() ,则该组数据的方差也是
,则该组数据的方差也是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的![]() 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为
个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为![]() ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当![]() 取何值时,有3个坑要补播种的概率最大?最大概率为多少?
取何值时,有3个坑要补播种的概率最大?最大概率为多少?
(2)当![]() 时,用
时,用![]() 表示要补播种的坑的个数,求
表示要补播种的坑的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com