
【题目】已知![]() 的顶点
的顶点![]() ,
,![]() 边上的高所在的直线的方程为
边上的高所在的直线的方程为![]() ,
,![]() 为
为![]() 中点,且
中点,且![]() 所在的直线的方程为
所在的直线的方程为![]() .
.
(1)求![]() 边所在的直线方程;
边所在的直线方程;
(2)求![]() 边所在的直线方程.
边所在的直线方程.
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班60人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 60 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为12的样本,则抽到喜好体育运动的人数为7.
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.001的前提下认为喜好体育运动与性别有关?说明你的理由;
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: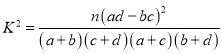 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲是某商店2018年(按360天计算)的日盈利额(单位:万元)的统计图.
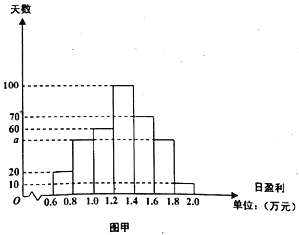
(1)请计算出该商店2018年日盈利额的平均值(精确到0.1,单位:万元):
(2)为了刺激消费者,该商店于2019年1月举行有奖促销活动,顾客凡购买一定金额的高品后均可参加抽奖.随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店对前5天抽奖活动的人数进行统计如下表:(![]() 表示第
表示第![]() 天参加抽奖活动的人数)
天参加抽奖活动的人数)
| 1 | 2 | 3 | 4 | 5 |
| 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(ⅰ)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() :
:
(ⅱ)该商店采取转盘方式进行抽奖(如图乙),其中转盘是个八等分的圆.每位顾客最多两次抽奖机会,若第一次抽到奖,则抽奖终止,若第一次未抽到奖,则再提供一次抽奖机会.抽到一等奖的奖品价值128元,抽到二等奖的奖品价值32元.若该商店此次抽奖活动持续7天,试估计该商店在此次抽奖活动结束时共送出价值为多少元的奖品(精确到0.1,单位:万元)?
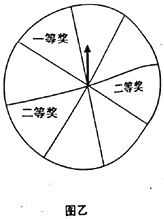
(3)用(1)中的2018年日盈利额的平均值去估计当月(共31天)每天的日盈利额.若商店每天的固定支出约为1000元,促销活动日的日盈利额比平常增加20%,则该商店当月的纯利润约为多少万元?(精确到0.1,纯利润=盈利额-固定支出-抽奖总奖金数)
参考公式及数据: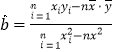 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数 ![]() 的图象上.
的图象上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足![]() ,若对任意
,若对任意![]() ,存在
,存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:①等比数列1,![]() ,
,![]() ,
,![]() ,…(
,…(![]() )的前
)的前![]() 项和为
项和为![]() ;②等差数列
;②等差数列![]() 中,若
中,若![]() ,
,![]() ,则该数列的前13项或14项之和最大;③若等差数列
,则该数列的前13项或14项之和最大;③若等差数列![]() 公差为
公差为![]() ,则其前
,则其前![]() 项和
项和![]() ;④若等比数列
;④若等比数列![]() 单调递增的充要条件是首项
单调递增的充要条件是首项![]() ,且公比
,且公比![]() ;⑤若数列
;⑤若数列![]() 满足
满足![]() ,
,![]() ,则
,则![]() .其中正确的是______(把你认为正确的命题序号都填上).
.其中正确的是______(把你认为正确的命题序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com