
【题目】某工厂生产![]() ,
,![]() ,
,![]() 三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
普通型 | 精品型 | |
纪念品 | 800 | 200 |
纪念品 |
| 150 |
纪念品 | 500 | 350 |
现采用分层抽样的方法在这一天生产的纪念品中抽取100个,其中有![]() 种纪念品40个.
种纪念品40个.
(1)若再用分层抽样的方法在所有![]() 种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
(2)从![]() 种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,
种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,![]() ,
,![]() ,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求
,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求![]() 的值.
的值.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
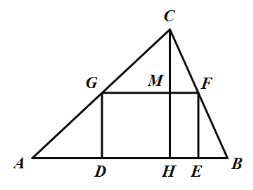
【题目】某市有一面积为12000平方米的三角形地块![]() ,其中边
,其中边![]() 长为200米,现计划建一个如图所示的长方形停车场
长为200米,现计划建一个如图所示的长方形停车场![]() ,停车场的四个顶点都在
,停车场的四个顶点都在![]() 的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设
的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设![]() 米,建设工程的总费用为
米,建设工程的总费用为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数表达式:
的函数表达式:
(2)求停车场面积最大时![]() 的值,并求此时的工程总费用.
的值,并求此时的工程总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() ,
,![]() ,
,![]() 等8人中选出5人排成一排.
等8人中选出5人排成一排.
(1)![]() 必须在内,有多少种排法?
必须在内,有多少种排法?
(2)![]() ,
,![]() ,
,![]() 三人不全在内,有多少种排法?
三人不全在内,有多少种排法?
(3)![]() ,
,![]() ,
,![]() 都在内,且
都在内,且![]() ,
,![]() 必须相邻,
必须相邻,![]() 与
与![]() ,
,![]() 都不相邻,都多少种排法?
都不相邻,都多少种排法?
(4)![]() 不允许站排头和排尾,
不允许站排头和排尾,![]() 不允许站在中间(第三位),有多少种排法?
不允许站在中间(第三位),有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公差不为零的等差数列![]() 中,
中,![]() ,
,![]() ,
,![]() 成等比数列,且该数列的前10项和为100,数列
成等比数列,且该数列的前10项和为100,数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() .
.
![]() Ⅰ
Ⅰ![]() 求数列
求数列![]() ,
,![]() 的通项公式;
的通项公式;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为1.记
的首项为1.记![]() .
.
(1)若![]() 为常数列,求
为常数列,求![]() 的值:
的值:
(2)若![]() 为公比为2的等比数列,求
为公比为2的等比数列,求![]() 的解析式:
的解析式:
(3)是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立?若存在,求出数列
都成立?若存在,求出数列![]() 的通项公式:若不存在,请说明理由.
的通项公式:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有10个除颜色外完全一样的黑球和白球,已知从袋中任意摸出2个球,至少得到1个白球的概率是![]() .
.
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为![]() ,已知
,已知![]() 且
且![]() .
.
(1)求角![]() ;
;
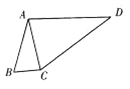
(2)如图,D为△ABC外一点,若在平面四边形ABCD中,![]() ,求△ACD面积的最大值.
,求△ACD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com