
过点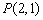 作直线l分别交x、y正半轴于A、B两点,当
作直线l分别交x、y正半轴于A、B两点,当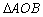 面积最小时,直线l的方程为____________.
面积最小时,直线l的方程为____________.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
定义域为R的偶函数f(x)满足对∀x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)与函数y=loga(x+1)在x∈(0,+∞)上至少有三个交点,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
若集合{ a,b,c,d}={1,2,3,4},且下列四个关系:①a=1;②b≠1;③c=2;④d≠4有且只有一个是正确的,则符合条件的有序数组(a,b,c,d)的个数是________.
a,b,c,d}={1,2,3,4},且下列四个关系:①a=1;②b≠1;③c=2;④d≠4有且只有一个是正确的,则符合条件的有序数组(a,b,c,d)的个数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义域为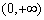 的函数
的函数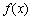 满足:对任意
满足:对任意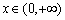 ,恒有
,恒有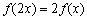 成立;当
成立;当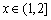 时,
时,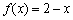 .给出如下结论:
.给出如下结论:
①对任意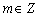 ,有
,有 ;
;
②函数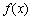 的值域为
的值域为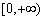 ;
;
③存在 ,使得
,使得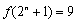 ;
;
④“函数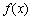 在区间
在区间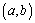 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在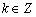 ,使得
,使得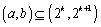 ”,
”,
其中所有正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com