
分析 (1)根据身高X服从正态分布N(160,ξ2),计算出P(170≤X<180)的值即可;
(2)求出P(150≤X<170)的值,由ξ服从二项分布B(3,0.6),求出对应的概率值,得出随机变量ξ的分布列,计算Eξ即可.
解答 解:(1)全市高三学生身高X(单位:cm)服从正态分布N(160,ξ2),
已知P(X<150)=0.2,
P(160≤x<170)=P(150≤X<160)=0.5-0.2=0.3,
P(X≥180)=0.03;
所以P(170≤X<180)=0.5-0.3-0.03=0.17;
故从该市高三学生中随机抽取一位学生,求该学生身高在区间[170,180)的概率为0.17;
(2)P(150≤X<170)=P(150≤X<160)+P(160≤X<170)=0.3+0.3=0.6,
所以ξ服从二项分布B(3,0.6),
P(ξ=0)=(1-0.6)3=0.064,
P(ξ=1)=3×0.6×(1-0.6)2=0.228,
P(ξ=2)=3×0.62×(1-0.6)=0.432,
P(ξ=3)=0.63=0.216,
所以随机变量ξ的分布列是
| ξ | 0 | 1 | 2 | 3 |
| P | 0.064 | 0.288 | 0.432 | 0.216 |
点评 本题考查了离散型随机就是的分布列和数学期望的应用问题,解题时要注意二项分布的性质的合理运用,是中档题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
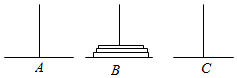 如图,汉诺塔问题是指有3根杆子A,B,C,杆上有若干碟子,把所有的碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面,把B杆上的3个碟子全部移动到A杆上,则最少需要移动的次数是( )
如图,汉诺塔问题是指有3根杆子A,B,C,杆上有若干碟子,把所有的碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面,把B杆上的3个碟子全部移动到A杆上,则最少需要移动的次数是( )| A. | 12 | B. | 9 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若T2n+1>0,则a1>0 | B. | 若T2n+1<0,则a1<0 | ||
| C. | 若T3n+1<0,则a1>0 | D. | 若T4n+1<0,则a1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com