
| A. | 若T2n+1>0,则a1>0 | B. | 若T2n+1<0,则a1<0 | ||
| C. | 若T3n+1<0,则a1>0 | D. | 若T4n+1<0,则a1<0 |
分析 举例说明A、B、C选项错误,再根据乘积的符号法则说明D选项正确.
解答 解:等比数列{an}中,Tn=a1a2…an,n∈N*,
对于A,令a1=-1,a2=1,a3=-1,有T3=1>0,但a1>0不成立,命题错误;
对于B,令a1=1,a2=-1,a3=1,有T3=-1<0,但a1<0不成立,命题错误;
对于C,令a1=a2=…a7=-1,有T7=-1<0,但a1>0不成立,命题错误;
对于D,T4n+1是a1,a3,…,a4n+1共2n+1项与a2,a4,…,a4n共2n项的乘积,
若T4n+1<0,则a1,a3,…,a4n+1的乘积<0,即a1<0,命题正确.
故选:D.
点评 本题考查了等比数列各项乘积的符号判断问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
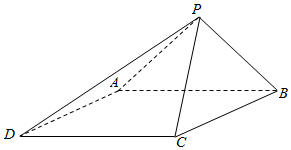 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c | B. | (1,2] | C. | [-1,1) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com