
分析 根据函数的定义域,直接只求出函数的值域.
解答 解:函数y=$\sqrt{3x+6}$-$\sqrt{8-x}$的定义域为:
$\left\{\begin{array}{l}{3x+6≥0}\\{8-x≥0}\end{array}\right.$
解得$\left\{\begin{array}{l}{x≥-2}\\{x≤8}\end{array}\right.$
∴函数y=$\sqrt{3x+6}$-$\sqrt{8-x}$的定义域为[-2,8].
当x=-2时,y=$\sqrt{3x+6}$-$\sqrt{8-x}$=$\sqrt{3×(-2)+6}$-$\sqrt{8-(-2)}$=-$\sqrt{10}$;
当x=8时,y=$\sqrt{3x+6}$-$\sqrt{8-x}$=$\sqrt{3×8+6}$-$\sqrt{8-8}$=$\sqrt{30}$
函数y=$\sqrt{3x+6}$-$\sqrt{8-x}$值域为[-$\sqrt{10}$,$\sqrt{30}$].
故答案为[-$\sqrt{10}$,$\sqrt{30}$].
点评 本题考查求函数值域的方法,体现直接法的数学思想.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{2}$<x<1} | B. | {x|$\frac{1}{2}$≤x<1} | C. | {x|$\frac{1}{2}$<x≤1} | D. | {x|$\frac{1}{2}$≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
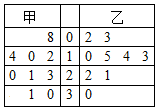 统计甲、乙两名运动员9场比赛得分情况得到茎叶图如图所示,设甲、乙得分平均数分别为$\overline{x}$,$\overline{y}$,中位数分别为m,n,则下列判断正确的是( )
统计甲、乙两名运动员9场比赛得分情况得到茎叶图如图所示,设甲、乙得分平均数分别为$\overline{x}$,$\overline{y}$,中位数分别为m,n,则下列判断正确的是( )| A. | $\overline{x}$<$\overline{y}$,m<n | B. | $\overline{x}$>$\overline{y}$,m<n | C. | $\overline{x}$>$\overline{y}$,m>n | D. | $\overline{x}$<$\overline{y}$,m>n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A?B | B. | A?B | C. | A=B | D. | A?B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c | B. | (1,2] | C. | [-1,1) | D. | (-1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com