
【题目】(Ⅰ)解不等式|6﹣|2x+1||>1; (Ⅱ)若关于x的不等式|x+1|+|x﹣1|+3+x<m有解,求实数m的取值范围.
【答案】解:(Ⅰ)∵|6﹣|2x+1||>1, ∴|2x+1|>7或|2x+1|<5,
解得:x>3或x<﹣4或﹣3<x<2,
故原不等式的解集是{x|x>3或x<﹣4或﹣3<x<2};
(Ⅱ)∵|x+1|+|x﹣1|+3+x<m,
∴x≥1时,x+1+x﹣1+3+x<m,
解得:x< ![]() ,
,
若关于x的不等式|x+1|+|x﹣1|+3+x<m有解,
故 ![]() >1,解得:m>6,
>1,解得:m>6,
﹣1<x<1时,x+1+1﹣x+3+x<m,
解得:x<m﹣5,
若关于x的不等式|x+1|+|x﹣1|+3+x<m有解,
故m﹣5>1,解得:m>6,
m≤﹣1时,﹣x﹣1+1﹣x+3+x<m,
解得:x>3﹣m,
若关于x的不等式|x+1|+|x﹣1|+3+x<m有解,
故3﹣m<﹣1,解得:m>4,
综上,实数m的取值范围(4,+∞)
【解析】(Ⅰ)通过讨论x的范围,求出不等式的解集即可;(Ⅱ)通过讨论x的范围,去掉绝对值,求出不等式的解集,得到关于m的不等式,取并集即可.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知一四棱锥P﹣ABCD的三视图如图所示,E是侧棱PC上的动点. 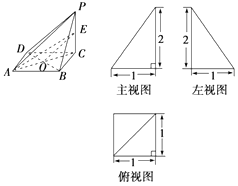
(Ⅰ)求四棱锥P﹣ABCD的体积.
(Ⅱ)若点E为PC的中点,AC∩BD=O,求证:EO∥平面PAD;
(Ⅲ)是否不论点E在何位置,都有BD⊥AE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点F(1,0),动点P(异于原点)在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且 ![]() ,
, ![]() .
.
(1)求动点N的轨迹C的方程;
(2)若直线l与动点N的轨迹交于A、B两点,若 ![]() 且
且 ![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点P,Q从点A(1,0)出发沿单位圆运动,点P按逆时针方向每秒钟转 ![]() 弧度,点Q按顺时针方向每秒钟转
弧度,点Q按顺时针方向每秒钟转 ![]() 弧度,设P,Q第一次相遇时在点B,则B点的坐标为 .
弧度,设P,Q第一次相遇时在点B,则B点的坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 2 | ﹣2 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:四棱锥P﹣ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1, ![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 
(1)证明:当点E在边BC上移动时,总有EF⊥AF;
(2)当CE等于何值时,PA与平面PDE所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的奇函数,且当x≥0时,f(x)=x2﹣(a+4)x+a.
(1)求实数a的值及f(x)的解析式;
(2)求使得f(x)=x+6成立的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中, ①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
A.③
B.③④
C.①③
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com