
【题目】已知![]() ,点
,点![]() 在第一象限,以
在第一象限,以![]() 为直径的圆与
为直径的圆与![]() 轴相切,动点
轴相切,动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若曲线![]() 在点
在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求满足
,求满足![]() 的点
的点![]() 的个数.
的个数.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直线x=﹣2上有一动点Q,过点Q作直线l,垂直于y轴,动点P在l1上,且满足![]() (O为坐标原点),记点P的轨迹为C.
(O为坐标原点),记点P的轨迹为C.
(1)求曲线C的方程;
(2)已知定点M(![]() ,0),N(
,0),N(![]() ,0),点A为曲线C上一点,直线AM交曲线C于另一点B,且点A在线段MB上,直线AN交曲线C于另一点D,求△MBD的内切圆半径r的取值范围.
,0),点A为曲线C上一点,直线AM交曲线C于另一点B,且点A在线段MB上,直线AN交曲线C于另一点D,求△MBD的内切圆半径r的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明下班回家途经3个有红绿灯的路口,交通法规定:若在路口遇到红灯,需停车等待;若在路口没遇到红灯,则直接通过.经长期观察发现:他在第一个路口遇到红灯的概率为![]() ,在第二、第三个道口遇到红灯的概率依次减小,在三个道口都没遇到红灯的概率为
,在第二、第三个道口遇到红灯的概率依次减小,在三个道口都没遇到红灯的概率为![]() ,在三个道口都遇到红灯的概率为
,在三个道口都遇到红灯的概率为![]() ,且他在各路口是否遇到红灯相互独立.
,且他在各路口是否遇到红灯相互独立.
(1)求小明下班回家途中至少有一个道口遇到红灯的概率;
(2)求小明下班回家途中在第三个道口首次遇到红灯的概率;
(3)记![]() 为小明下班回家途中遇到红灯的路口个数,求数学期望
为小明下班回家途中遇到红灯的路口个数,求数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司在![]() 年年初准备将
年年初准备将![]() 万元投资到“低碳”项目上,现有两个项目供选择:
万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利![]() ,也可能亏损
,也可能亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利![]() ,可能损失
,可能损失![]() ,也可能不赔不赚,且这三种情况发生的概率分别为
,也可能不赔不赚,且这三种情况发生的概率分别为![]() 、
、![]() 和
和![]() .
.
针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为()
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A.2.6天B.2.2天C.2.4天D.2.8天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]()
![]() 中,对任何正整数n都有:
中,对任何正整数n都有: ![]()
(1)若数列![]() 是首项和公差都是1的等差数列,求证:数列
是首项和公差都是1的等差数列,求证:数列![]() 是等比数列;
是等比数列;
(2)若数列![]() 是首项为1的等比数列,数列
是首项为1的等比数列,数列![]() 是否是等差数列?若是请求出通项公式.
是否是等差数列?若是请求出通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的焦距是
的焦距是![]() ,长轴长是短轴长3倍,任作斜率为
,长轴长是短轴长3倍,任作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(如图所示),且点
两点(如图所示),且点![]() 在直线
在直线![]() 的左上方.
的左上方.

(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)证明:![]() 的内切圆的圆心在一条定直线上。
的内切圆的圆心在一条定直线上。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了使房价回归到收入可支撑的水平,让全体人民住有所居,近年来全国各一、二线城市打击投机购房,陆续出台了住房限购令.某市一小区为了进一步了解已购房民众对市政府岀台楼市限购令的认同情况,随机抽取了本小区50户住户进行调查,各户人平均月收入(单位:千元)的户数频率分布直方图如图,其中赞成限购的户数如下表:
人平均月收入 |
|
|
|
|
|
|
赞成户数 | 4 | 9 | 12 | 6 | 3 | 1 |
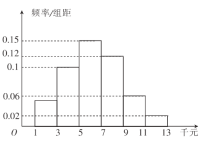
(1)若从人平均月收入在![]() 的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
(2)若将小区人平均月收入不低于7千元的住户称为“高收入户”,人平均月收入低于7千元的住户称为“非高收入户”根据已知条件完成如图所给的![]() 列联表,并说明能否有
列联表,并说明能否有![]() 的把握认为“收入的高低”与“赞成楼市限购令”有关.
的把握认为“收入的高低”与“赞成楼市限购令”有关.
非高收入户 | 高收入户 | ||
赞成 | |||
不赞成 | |||
总计 |
附:临界值表
| 0.1 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.63.5 | 10.828 |
参考公式: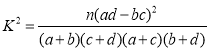 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com