
【题目】某单位年会进行抽奖活动,在抽奖箱里装有![]() 张印有“一等奖”的卡片,
张印有“一等奖”的卡片, ![]() 张印
张印
有“二等奖”的卡片, 3张印有“新年快乐”的卡片,抽中“一等奖”获奖![]() 元, 抽中“二等奖”获奖
元, 抽中“二等奖”获奖![]() 元,抽中“新年快乐”无奖金.
元,抽中“新年快乐”无奖金.
(1)单位员工小张参加抽奖活动,每次随机抽取一张卡片,抽取后不放回.假如小张一定要将所有获奖卡片全部抽完才停止. 记![]() 表示“小张恰好抽奖
表示“小张恰好抽奖![]() 次停止活动”,求
次停止活动”,求![]() 的值;
的值;
(2)若单位员工小王参加抽奖活动,一次随机抽取![]() 张卡片.
张卡片.
①![]() 记
记![]() 表示“小王参加抽奖活动中奖”,求
表示“小王参加抽奖活动中奖”,求![]() 的值;
的值;
②设![]() 表示“小王参加抽奖活动所获奖金数(单位:元)”,求
表示“小王参加抽奖活动所获奖金数(单位:元)”,求![]() 的分布列和数学期望.
的分布列和数学期望.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】春节过后,某市教育局从全市高中生中抽去了100人,调查了他们的压岁钱收入情况,按照金额(单位:百元)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .统计结果如下表所示:
.统计结果如下表所示:
![]()
该市高中生压岁钱收入![]() 可以认为服从正态分布
可以认为服从正态分布![]() ,用样本平均数
,用样本平均数![]() (每组数据取区间的中点值)作为
(每组数据取区间的中点值)作为![]() 的估计值.
的估计值.
(1)求样本平均数![]() ;
;
(2)求![]() ;
;
(3)某文化公司赞助了市教育局的这次社会调查活动,并针对该市的高中生制定了赠送“读书卡”的活动,赠送方式为:压岁钱低于![]() 的获赠两次读书卡,压岁钱不低于
的获赠两次读书卡,压岁钱不低于![]() 的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:
的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:

现从该市高中生中随机抽取一人,记![]() (单位:张)为该名高中生获赠的读书卡的张数,求
(单位:张)为该名高中生获赠的读书卡的张数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图
(如图![]() )的平面展开图(如图
)的平面展开图(如图![]() )中,四边形
)中,四边形![]() 为边长为
为边长为![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线![]() 的焦点重合,过点
的焦点重合,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆过坐标原点
为直径的圆过坐标原点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市家庭用电量的情况,该市统计局调查了200户居民去年一年的月均用电量(单位:kWh),数据从小到大排序如下:
8 18 22 31 42 48 49 50 51 56 57 57 60 61 61
61 62 62 63 63 65 66 67 69 70 70 71 72 72 74
76 77 77 78 78 80 80 82 82 82 83 84 84 88 88
89 90 91 93 93 94 95 96 96 96 97 98 98 98 99
100 100 100 101 101 101 105 106 106 106 107
107 107 107 108 108 109 109 110 110 110 111
112 113 113 114 115 116 118 120 120 120 121
123 124 127 127 127 130 130 130 131 131 132
132 132 133 133 134 134 134 135 135 135 135
136 137 137 138 139 139 140 141 142 144 146
146 147 148 149 151 152 154 156 159 160 162
163 163 164 165 167 169 170 170 172 174 174
177 178 178 180 182 182 187 189 191 191 192
194 194 200 201 201 202 203 203 206 208 212
213 214 216 223 224 237 247 250 250 251 253
254 258 260 265 274 274 283 288 289 304 319
320 324 339 462 498 530 542 626
为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,请确定各档的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() ,
,![]() 是线段
是线段![]() 上一点.
上一点.
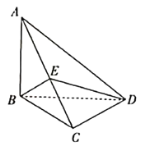
(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(2)是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,请指出点
?若存在,请指出点![]() 的位置,并加以证明;若不存在,请说明理由.
的位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com