练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若一三角形三边所在的直线方程分别为x+2y﹣5=0，y﹣2=0，x+y﹣4=0，则能够覆盖此三角形且面积最小的圆的方程为 ．

    【答案】（x﹣2）2+（y﹣1.5）2=6.25
    【解析】解：∵三角形三边所在的直线方程分别为x+2y﹣5=0，y﹣2=0，x+y﹣4=0，
    ∴可得三角形的三个顶点分别是A（1，2），B（2，2），C（3，1），△ABC为钝角三角形
    能够覆盖此三角形且面积最小是以AC为直径的圆，方程为（x﹣2）2+（y﹣1.5）2=6.25．
    所以答案是：（x﹣2）2+（y﹣1.5）2=6.25
    【考点精析】关于本题考查的圆的标准方程，需要了解圆的标准方程：；圆心为A(a,b),半径为r的圆的方程才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别是角A，B，C的对边，A，B是锐角，c=10，且 ．
    （1）证明角C=90°；
    （2）求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正项数列{an}的前n项和Sn满足：Sn2﹣（n2+n﹣1）Sn﹣（n2+n）=0
    （1）求数列{an}的通项公式an；
    （2）令bn= ，求数列{bn}的前n项和Tn ， 证明：对于任意的n∈N* ， 都有Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知α是第三象限角，且sinα=﹣ ．
    （1）求tanα与tan（α﹣ ）的值；
    （2）求cos2α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若某校高一年级8个班参加合唱比赛的得分如茎叶图所示，则这组数据的中位数和平均数分别是（ ）

    A.91.5和91.5
    B.91.5和92
    C.91和91.5
    D.92和92

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB= ，AF=1，M是线段EF的中点．

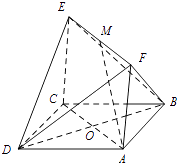
    （1）求证：AM∥平面BDE；
    （2）求证：AM⊥平面BDF；
    （3）求A点到面BDF的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017南通扬州泰州苏北四市高三二模】（本小题满分14分）

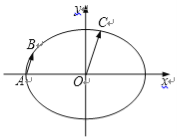
    如图，在平面直角坐标系中，已知椭圆的离心率为，C为椭

    圆上位于第一象限内的一点．

    （1）若点的坐标为，求a，b的值；

    （2）设A为椭圆的左顶点，B为椭圆上一点，且，求直线AB的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

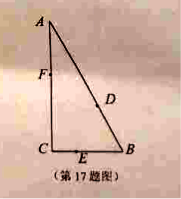
    【题目】【2017镇江一模】如图，某公园有三条观光大道围成直角三角形，其中直角边，

    斜边．现有甲、乙、丙三位小朋友分别在大道上嬉戏，所在位

    置分别记为点．

    （1）若甲乙都以每分钟的速度从点出发在各自的大道上奔走，到大道的另一端

    时即停，乙比甲迟分钟出发，当乙出发分钟后，求此时甲乙两人之间的距离；

    （2）设，乙丙之间的距离是甲乙之间距离的倍，且，请将甲

    乙之间的距离表示为的函数，并求甲乙之间的最小距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在平面坐标系内，O为坐标原点，向量 =（1，7）， =（5，1）， =（2，1），点M为直线OP上的一个动点．
    （1）当 取最小值时，求向量 的坐标；
    （2）在点M满足（I）的条件下，求∠AMB的余弦值．

    查看答案和解析>>

    同步练习册答案