
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,A,B是锐角,c=10,且 ![]() .
.
(1)证明角C=90°;
(2)求△ABC的面积.
【答案】
(1)证明:在△ABC中,∵ ![]() .
.
∴根据正弦定理得 ![]() ,整理为sinAcosA=sinBcosB,即sin2A=sin2B.
,整理为sinAcosA=sinBcosB,即sin2A=sin2B.
∵0<2A,2B<π,
∴2A=2B,或2A+2B=π.
∵ ![]() ,A≠B,
,A≠B,
∴A+B= ![]() ,即∠C=90°
,即∠C=90°
(2)解:∵△ABC是以角C为直角的直角三角形,且c=10, ![]() ,a2+b2=c2,
,a2+b2=c2,
∴可得:( ![]() a)2+a2=100,
a)2+a2=100,
∴求得a=6,b=8.
∴△ABC的面积S= ![]() ab=24.
ab=24.
【解析】(1)根据正弦定理,二倍角公式化简已知可得sin2A=sin2B,结合角的范围可得2A=2B,或2A+2B=π,由 ![]() ,可得A≠B,从而可求A+B=
,可得A≠B,从而可求A+B= ![]() ,即可得解.(2)由(1)及已知,利用勾股定理可求a,b的值,进而利用三角形面积公式即可计算得解.
,即可得解.(2)由(1)及已知,利用勾股定理可求a,b的值,进而利用三角形面积公式即可计算得解.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 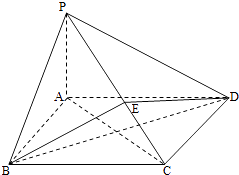
(1)证明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)当a=﹣1时,求函数f(x)的单调递增区间;
(2)求实数a的取值范围,使y=f(x)在区间[﹣5,5]上是单调函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】已知椭圆![]() :
:![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
:![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)分别过![]() 、
、![]() 作平行直线
作平行直线![]() 、
、![]() ,若直线
,若直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,直线
无公共点,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,其中点
两点,其中点![]() ,
,![]() 在
在![]() 轴上方,求四边形
轴上方,求四边形![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公差不为零的等差数列{an}中,a3=7,又a2 , a4 , a9成等比数列.
(1)求数列{an}的通项公式.
(2)设bn=2 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com