
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)当a=﹣1时,求函数f(x)的单调递增区间;
(2)求实数a的取值范围,使y=f(x)在区间[﹣5,5]上是单调函数.
【答案】
(1)解:当a=﹣1时,f(x)=x2﹣2x+2=(x﹣1)2+1,
图象是抛物线,且开口向上,对称轴是x=1,
所以,当x∈[﹣5,5]时,f(x)的单调递减区间是[﹣5,1],单调递增区间是[1,5]
(2)解:∵f(x)=x2+2ax+2,图象是抛物线,且开口向上,对称轴是x=﹣a;
当x∈[﹣5,5]时,若﹣a≤﹣5,即a≥5时,f(x)单调递增;
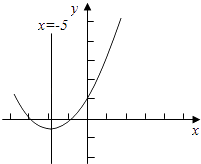
若﹣a≥5,即a≤﹣5时,f(x)单调递减;
所以,f(x)在[﹣5,5]上是单调函数时,
a的取值范围是(﹣∞,﹣5]∪[5,+∞)
【解析】(1)将a=﹣1的值代入函数的解析式,求出函数的对称轴,从而求出函数的单调区间;(2)先求出函数的对称轴,通过讨论a的范围,得到函数的单调性,进而求出满足条件的a的范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


科目:高中数学 来源: 题型:
【题目】已知a,b,c都是正数,
(1)若a+c=1,试比较a3+a2c+ab2+b2c与a2b+abc的大小;
(2)若a2+b2+c2=1,求证: ![]() ﹣
﹣ ![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义实数a,b间的计算法则如下a△b= ![]() .
.
(1)计算2△(3△1);
(2)对0<x<z<y的任意实数x,y,z,判断x△(y△z)与(x△y)△z的大小,并说明理由;
(3)写出函数y=(1△x)+(2△x),x∈R的解析式,作出该函数的图象,并写出该函数单调递增区间和值域(只需要写出结果). 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求适合下列条件的圆锥曲线的标准方程:
(1)焦点坐标为( ![]() ,0),准线方程为x=
,0),准线方程为x= ![]() 的椭圆;
的椭圆;
(2)过点( ![]() ,2),渐近线方程为y=±2x的双曲线.
,2),渐近线方程为y=±2x的双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接“双十一”活动,某网店需要根据实际情况确定经营策略.
(1)采购员计划分两次购买一种原料,第一次购买时价格为a元/个,第二次购买时价格为b元/个(其中a≠b).该采购员有两种方案:方案甲:每次购买m个;方案乙:每次购买n元.请确定按照哪种方案购买原料平均价格较小.
(2)“双十一”活动后,网店计划对原价为100元的商品两次提价,现有两种方案:方案丙:第一次提价p,第二次提价q;方案丁:第一次提价 ![]() ,第二次提价
,第二次提价 ![]() ,(其中p≠q)请确定哪种方案提价后价格较高.
,(其中p≠q)请确定哪种方案提价后价格较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.![]()
C.(1,3]
D.(1,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列{an}的前n项和Sn满足:Sn2﹣(n2+n﹣1)Sn﹣(n2+n)=0
(1)求数列{an}的通项公式an;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn
,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com