
【题目】设函数f(x)=x3﹣6x+5,x∈R.
(1)求f(x)的单调区间和极值;
(2)求曲线f(x)过点(1,0)的切线方程.
【答案】
(1)解:f'(x)=3(x2﹣2),
令f'(x)=0,得 ![]() ,
,
∴当 ![]() 或
或 ![]() 时,f'(x)>0;
时,f'(x)>0;
当 ![]() 时,f'(x)<0,
时,f'(x)<0,
∴f(x)的单调递增区间是 ![]() 和
和 ![]() ,
,
单调递减区间是 ![]() ;
;
当x=﹣ ![]() ,f(x)有极大值5+4
,f(x)有极大值5+4 ![]() ;当x=
;当x= ![]() ,f(x)有极小值5﹣4
,f(x)有极小值5﹣4 ![]()
(2)解:设切点为(m,n),
则切线的斜率为3(m2﹣2),
切线的方程为y﹣(m3﹣6m+5)=3(m2﹣2)(x﹣m),
代入(1,0),可得﹣(m3﹣6m+5)=3(m2﹣2)(1﹣m),
化为(m﹣1)2(2m+1)=0,
解得m=1或m=﹣ ![]() ,
,
则斜率为﹣3或﹣ ![]() ,
,
可得切线的方程为y=﹣3x+3或y=﹣ ![]() x+
x+ ![]()
【解析】(1)求导f(x)导数,可得极值点,导数大于0可得增区间;导数小于0可得减区间;进而得到极值;(2)设切点为(m,n),可得切线的斜率,切线方程,代入(1,0),解方程可得切点,进而得到所求切线方程.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为:
 ,
, ![]() ,其中
,其中![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 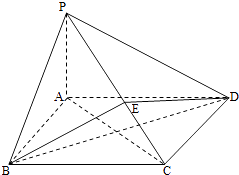
(1)证明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y= ![]() 的图象上存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形(其中O为坐标原点),且斜边的中点恰好在y轴上,则实数a的取值范围是 .
的图象上存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形(其中O为坐标原点),且斜边的中点恰好在y轴上,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx.
(1)求函数g(x)=f(x+1)﹣x的最大值;
(2)若对任意x>0,不等式f(x)≤ax≤x2+1恒成立,求实数a的取值范围;
(3)若x1>x2>0,求证: ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)当a=﹣1时,求函数f(x)的单调递增区间;
(2)求实数a的取值范围,使y=f(x)在区间[﹣5,5]上是单调函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】已知椭圆![]() :
:![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
:![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)分别过![]() 、
、![]() 作平行直线
作平行直线![]() 、
、![]() ,若直线
,若直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,直线
无公共点,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,其中点
两点,其中点![]() ,
,![]() 在
在![]() 轴上方,求四边形
轴上方,求四边形![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com