
【题目】已知函数f(x)=lnx.
(1)求函数g(x)=f(x+1)﹣x的最大值;
(2)若对任意x>0,不等式f(x)≤ax≤x2+1恒成立,求实数a的取值范围;
(3)若x1>x2>0,求证: ![]() >
> ![]() .
.
【答案】
(1)解:∵f(x)=lnx,
∴g(x)=f(x+1)﹣x=ln(x+1)﹣x,x>﹣1,
∴ ![]() .
.
当x∈(﹣1,0)时,g′(x)>0,∴g(x)在(﹣1,0)上单调递增;
当x∈(0,+∞)时,g′(x)<0,则g(x)在(0,+∞)上单调递减,
∴g(x)在x=0处取得最大值g(0)=0
(2)解:∵对任意x>0,不等式f(x)≤ax≤x2+1恒成立,
∴ 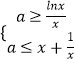 在x>0上恒成立,
在x>0上恒成立,
进一步转化为 ![]() ,
,
设h(x)= ![]() ,则
,则 ![]() ,
,
当x∈(1,e)时,h′(x)>0;当x∈(e,+∞)时,h′(x)<0,
∴h(x) ![]() .
.
要使f(x)≤ax恒成立,必须a ![]() .
.
另一方面,当x>0时,x+ ![]() ,
,
要使ax≤x2+1恒成立,必须a≤2,
∴满足条件的a的取值范围是[ ![]() ,2]
,2]
(3)解:当x1>x2>0时, ![]() >
> ![]() 等价于
等价于 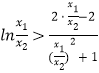 .
.
令t= ![]() ,设u(t)=lnt﹣
,设u(t)=lnt﹣ ![]() ,t>1
,t>1
则 ![]() >0,
>0,
∴u(t)在(1,+∞)上单调递增,
∴u(t)>u(1)=0,
∴ ![]() >
> ![]()
【解析】(1)先求出g(x)=ln(x﹣1)﹣x(x>﹣1),然后求导确定单调区间,极值,最值即可求.(2)本小题转化为 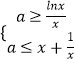 在x>0上恒成立,进一步转化为
在x>0上恒成立,进一步转化为 ![]() ,然后构造函数h(x)=
,然后构造函数h(x)= ![]() ,利用导数研究出h(x)的最大值,再利用基础不等式可知
,利用导数研究出h(x)的最大值,再利用基础不等式可知 ![]() ,从而可知a的取值范围.(3)本小题等价于
,从而可知a的取值范围.(3)本小题等价于 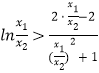 .令t=
.令t= ![]() ,设u(t)=lnt﹣
,设u(t)=lnt﹣ ![]() ,t>1,由导数性质求出u(t)>u(1)=0,由此能够证明
,t>1,由导数性质求出u(t)>u(1)=0,由此能够证明 ![]() >
> ![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程.
在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈[0,1],给出以下四个命题:
①平面MENF⊥平面BDD′B′;
②当且仅当x= ![]() 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
③四边形MENF周长l=f(x),x∈0,1]是单调函数;
④四棱锥C′﹣MENF的体积v=h(x)为常函数;
以上命题中真命题的序号为 . 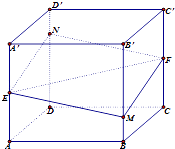
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义实数a,b间的计算法则如下a△b= ![]() .
.
(1)计算2△(3△1);
(2)对0<x<z<y的任意实数x,y,z,判断x△(y△z)与(x△y)△z的大小,并说明理由;
(3)写出函数y=(1△x)+(2△x),x∈R的解析式,作出该函数的图象,并写出该函数单调递增区间和值域(只需要写出结果). 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在(0,+∞)上的函数,且对任意的正实数x1 , x2均有:(x1﹣x2)[f(x1)﹣f(x2)]>0,则不等式f(x)﹣f(8x﹣16)>0的解集是( )
A.(0,+∞)
B.(0,2)
C.(2,+∞)
D.(2, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求适合下列条件的圆锥曲线的标准方程:
(1)焦点坐标为( ![]() ,0),准线方程为x=
,0),准线方程为x= ![]() 的椭圆;
的椭圆;
(2)过点( ![]() ,2),渐近线方程为y=±2x的双曲线.
,2),渐近线方程为y=±2x的双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.![]()
C.(1,3]
D.(1,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|. 
(1)求实数a,b间满足的等量关系;
(2)若以P为圆心的圆P与圆O有公共点,试求圆P的半径最小时圆P的方程;
(3)当P点的位置发生变化时,直线QM是否过定点,如果是,求出定点坐标,如果不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com