【题目】已知a，b，c都是正数，
（1）若a+c=1，试比较a3+a2c+ab2+b2c与a2b+abc的大小；
（2）若a2+b2+c2=1，求证： 
﹣ 
≥3．
【答案】
（1）解：∵a，b，c都是正数，且a+c=1，
∴a3+a2c+ab2+b2c﹣a2b﹣abc=（a2+b2﹣ab）（a+c）= 
＞0，
所以a3+a2c+ab2+b2c＞a2b+abc
（2）证明：∵a，b，c都是正数，且a2+b2+c2=1，
∴ 
﹣ 
=3+ 
≥3
当且仅当a=b=c= 
取得等号，即 ﹣ ≥3
【解析】（1）将两个式子作差变形，通过提取公因式，判断符号，得出大小关系；（2）利用配方法证明即可．
【考点精析】利用不等式的证明对题目进行判断即可得到答案，需要熟知不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．
名师金手指领衔课时系列答案科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，曲线
过点
，其参数方程为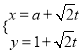
（
为参数， 
），以
为极点， 
轴非负半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线
的普通方程和曲线
的直角坐标方程；
（2）已知曲线
与曲线
交于
两点，且
，求实数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面四组函数中，f（x）与g（x）表示同一个函数的是（ ）
A.f（x）=|x|， 
B.f（x）=2x， 
C.f（x）=x， 
D.f（x）=x， 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某单位共有10名员工，他们某年的收入如下表：
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪（万元） | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
（1）求该单位员工当年年薪的平均值和中位数；
（2）从该单位中任取2人，此2人中年薪收入高于7万的人数记为
，求
的分布列和期望；
（3）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为4万元，5.5万元，6万元，8.5万元，预测该员工第五年的年薪为多少？
附：线性回归方程
中系数计算公式分别为：
， 
，其中
为样本均值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（n）=2n+1（n∈N*），集合A={1，2，3，4，5}，B={3，4，5，6，7}，记f（A）={n|f（n）∈A}，f（B）={m|f（m）∈B}，f（A）∩f（B）=（ ）
A.{1，2}
B.{1，2，3}
C.{3，5}
D.{3，5，7}
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】命题p：x∈R，ax2+ax﹣1＜0，命题q： 
+1＜0．
（1）若“p或q”为假命题，求实数a的取值范围；
（2）若“非q”是“α∈[m，m+1]”的必要不充分条件，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图四棱锥P﹣ABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD=CD=2 
，BC=4 ，PA=2，点M在线段PD上．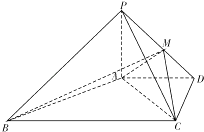 
（1）求证：AB⊥PC．
（2）若二面角M﹣AC﹣D的大小为45°，求BM与平面PAC所成的角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．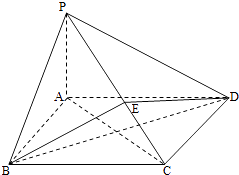 
（1）证明：BD⊥平面PAC；
（2）若PA=1，AD=2，求二面角B﹣PC﹣A的正切值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2+2ax+2，x∈[﹣5，5]．
（1）当a=﹣1时，求函数f（x）的单调递增区间；
（2）求实数a的取值范围，使y=f（x）在区间[﹣5，5]上是单调函数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com