练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知f（n）=2n+1（n∈N*），集合A={1，2，3，4，5}，B={3，4，5，6，7}，记f（A）={n|f（n）∈A}，f（B）={m|f（m）∈B}，f（A）∩f（B）=（ ）
    A.{1，2}
    B.{1，2，3}
    C.{3，5}
    D.{3，5，7}

    【答案】A
    【解析】解：∵f（n）=2n+1（n∈N*），集合A={1，2，3，4，5}，B={3，4，5，6，7}，记f（A）={n|f（n）∈A}，f（B）={m|f（m）∈B}，
    ∴f（A）∩f（B）={1，2}∩{1，2，3}={1，2}．
    故选：A．
    【考点精析】本题主要考查了集合的交集运算的相关知识点，需要掌握交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】△ABC中，角A，B，C所对的边分别为a，b，c，S表示三角形的面积，若asinA+bsinB=csinC，且S= ，则对△ABC的形状的精确描述是（ ）
    A.直角三角形
    B.等腰三角形
    C.等腰或直角三角形
    D.等腰直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】不等式ax2+bx+c＞0的解集为{x|﹣1＜x＜2}，则不等式a（x2+1）+b（x﹣1）+c＞2ax的解集为（ ）
    A.{x|0＜x＜3}
    B.{x|x＜0或x＞3}
    C.{x|﹣2＜x＜1}
    D.{x|x＜﹣2或x＞1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4－4：坐标系与参数方程．

    在平面直角坐标系中，倾斜角为的直线的参数方程为（为参数）.以坐标原点为极点，以轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程是.

    （1）写出直线的普通方程和曲线的直角坐标方程；

    （2）已知点.若点的极坐标为，直线经过点且与曲线相交于两点，设线段的中点为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列{an}中，已知a1=1，a2=2，an+2= （k∈N*）．
    （1）求数列{an}的通项公式；
    （2）求满足2an+1=an+an+2的正整数n的值；
    （3）设数列{an}的前n项和为Sn ， 问是否存在正整数m，n，使得S2n=mS2n﹣1？若存在，求出所有的正整数对（m，n）；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b，c都是正数，
    （1）若a+c=1，试比较a3+a2c+ab2+b2c与a2b+abc的大小；
    （2）若a2+b2+c2=1，求证： ﹣ ≥3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数集A={a1 ， a2…an}（0≤a1＜a2…＜an ， n≥2）具有性质P；对任意的 i，j（1≤i≤j≤n），ai+aj与aj﹣ai两数中至少有一个属于A．
    （1）分别判断数集{0，1，3，4}与{0，2，3，6}是否具有性质P，并说明理由；
    （2）证明：a1=0，且nan=2（a1+a2+a+..+an）
    （3）当n=5时若 a2=2，求集合A．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，正方体ABCD﹣A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′交于M、N，设BM=x，x∈[0，1]，给出以下四个命题：
    ①平面MENF⊥平面BDD′B′；
    ②当且仅当x= 时，四边形MENF的面积最小；
    ③四边形MENF周长l=f（x），x∈0，1]是单调函数；
    ④四棱锥C′﹣MENF的体积v=h（x）为常函数；
    以上命题中真命题的序号为 ．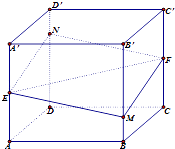

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求适合下列条件的圆锥曲线的标准方程：
    （1）焦点坐标为（ ，0），准线方程为x= 的椭圆；
    （2）过点（ ，2），渐近线方程为y=±2x的双曲线．

    查看答案和解析>>

    同步练习册答案