
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为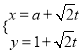 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _________,
_________, ![]() __________,
__________, ![]() _________.
_________.
猜想: ![]() _______.
_______.
然后用数学归纳法证明.证明过程如下:
①当![]() 时,________________,猜想成立
时,________________,猜想成立
②假设![]() (
(![]() N*)时,猜想成立,即
N*)时,猜想成立,即![]() _______.
_______.
那么,当![]() 时,由已知
时,由已知![]() ,得
,得![]() _________.
_________.
又![]() ,两式相减并化简,得
,两式相减并化简,得![]() _____________(用含
_____________(用含![]() 的代数式表示).
的代数式表示).
所以,当![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何![]() N*都成立.
N*都成立.
思路2:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _____________.
_____________.
由已知![]() ,写出
,写出![]() 与
与![]() 的关系式:
的关系式: ![]() _____________________,
_____________________,
两式相减,得![]() 与
与![]() 的递推关系式:
的递推关系式: ![]() ____________________.
____________________.
整理: ![]() ____________.
____________.
发现:数列![]() 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.
得出:数列![]() 的通项公式
的通项公式![]() ____,进而得到
____,进而得到![]() ____________.
____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当a=2时,求(x)在x∈[1,e2]时的最值(参考数据:e2≈7.4);
(Ⅱ)若![]() ,有f(x)+g(x)≤0恒成立,求实数a的值;
,有f(x)+g(x)≤0恒成立,求实数a的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数,当x>0时,解析式为f(x)=![]() .
.
(1)求f(x)在R上的解析式;
(2)用定义证明f(x)在(0,+∞)上为减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
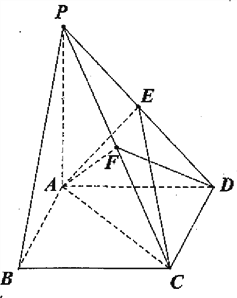
【题目】如图,四棱锥P—ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形,![]() ,求二面角C—AF—D大小.
,求二面角C—AF—D大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)求f(2)+f![]() ,f(3)+f
,f(3)+f![]() 的值;
的值;
(2)求证:f(x)+f![]() 是定值;
是定值;
(3)求f(2)+f![]() +f(3)+f
+f(3)+f![]() +…+
+…+![]() +f
+f![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com