
已知函数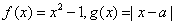 .
.
(1)当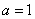 时,求
时,求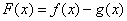 的零点;
的零点;
(2)若方程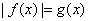 有三个不同的实数解,求
有三个不同的实数解,求 的值;
的值;
(3)求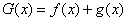 在
在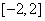 上的最小值
上的最小值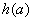 .
.
解答】:(1)当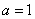 时,
时,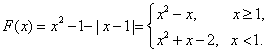 , ………2分
, ………2分
令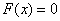 得,当
得,当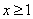 时,
时,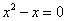 ,
,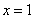 (
(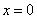 舍去)
舍去)
当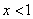 时,
时,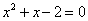 ,
,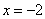 (
(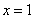 舍去)
舍去)
所以当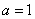 时,
时,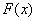 的零点为1,
的零点为1, ………………………………4分
………………………………4分
(2)方程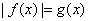 ,即
,即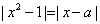 ,
,
变形得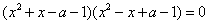 , ………………………………6分
, ………………………………6分
从而欲使原方程有三个不同的解,即要求方程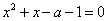 …(1)
…(1)
与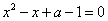 …(2)
…(2)
满足下列情形之一:
(I)一个有等根,另一个有两不等根,且三根不等
(II)方程(1)、(2)均有两不等根且由一根相同;
对情形(I):若方程(1)有等根,则
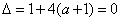 解得
解得 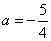 代入方程(2)检验符合;
代入方程(2)检验符合;
若方程(2)有等根,则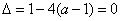 解得
解得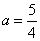 代入方程(1)检验符合;……8分
代入方程(1)检验符合;……8分
对情形(II):设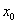 是公共根,则
是公共根,则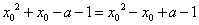 ,
,
解得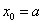 代入(1)得
代入(1)得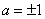 ,
,
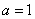 代入
代入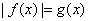 检验得三个解为-2、0、1符合
检验得三个解为-2、0、1符合
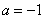 代入
代入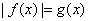 检验得三个解为2、0、-1符合
检验得三个解为2、0、-1符合
故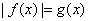 有三个不同的解的值为
有三个不同的解的值为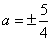 或
或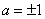 . ……………10分
. ……………10分
(3)因为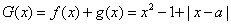 =
=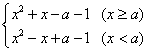 ,
,
① 当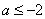 时
时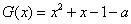 ,在
,在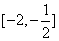 上递减,在
上递减,在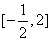 上递增,
上递增,
故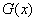 在
在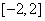 上最小值为
上最小值为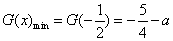 ………………11分
………………11分
② 当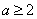 时
时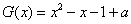 ,在
,在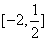 上递减,在
上递减,在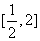 上递增,
上递增,
故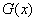 在
在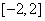 上最小值为
上最小值为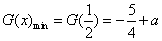 ………………12分
………………12分
③ 当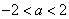 时,
时,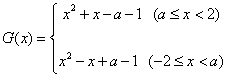
(i)当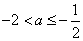 时,结合图形可知当
时,结合图形可知当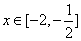 时递减,在
时递减,在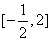 上递增
上递增
故此时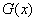 在[-2,2]上的最小值为
在[-2,2]上的最小值为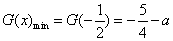 ………………13分
………………13分
(ii)当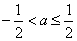 时,结合图形可知当
时,结合图形可知当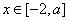 时递减,当
时递减,当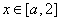 时递增,
时递增,
故此时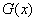 在[-2,2]上的最小值为
在[-2,2]上的最小值为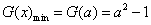 ……………………14分
……………………14分
(iii)当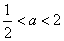 时,结合图形可知当
时,结合图形可知当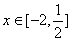 时递减,当
时递减,当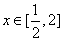 时递增,
时递增,
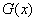 在
在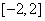 上最小值为
上最小值为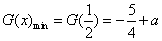 ………………………15分
………………………15分
综上所述: 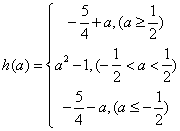 ………………………16分
………………………16分
解法二:因为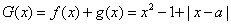 =
=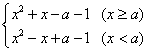 ,
,
① 当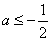 时,
时,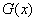 在
在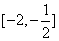 上递减,在
上递减,在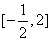 上递增,
上递增,
故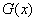 在
在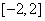 上最小值为
上最小值为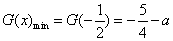 ………………12分
………………12分
② 当 时
时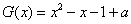 ,在
,在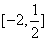 上递减,在
上递减,在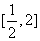 上递增,
上递增,
故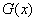 在
在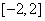 上最小值为
上最小值为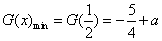 ………………14分
………………14分
③ 当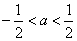 时,
时,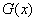 在
在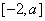 上递减,当
上递减,当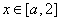 时递增,故此时
时递增,故此时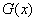 在[-2,2]上的最小值为
在[-2,2]上的最小值为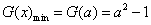
综上所述: 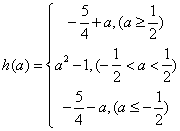


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
在篮球比赛中,某篮球队队员投进三分球的个数如表所示:
| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 |
|
|
|
|
|
|
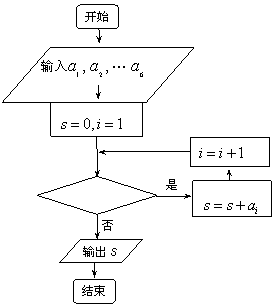
右图是统计上述6名队员在比赛中投进的三分球总数s的程序框图,则图中的判断框内应填入的条件是
A. 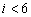 B.
B.  C.
C. 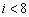 D.
D. 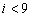
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com