
分析 (Ⅰ)将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求出ω,最后将内层函数看作整体,当$x∈[0,\frac{π}{2}]$时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值,即得到f(x)的值域.
(Ⅱ)利用f(C)=0求出角C的大小.在利用正弦定理可求b.
解答 解:(Ⅰ)函数f(x)=cos2ωx-2cos2(ωx+$\frac{π}{4}$)(ω>0)的化简可得:$f(x)=cos2ωx-[1+cos(2ωx+\frac{π}{2})]$=cos2ωx+sin2ωx-1=$\sqrt{2}sin(2ωx+\frac{π}{4})-1$.
∵函数f(x)的最小正周期T=π.
由$T=\frac{2π}{2ω}=π$,得ω=1,
∴$f(x)=\sqrt{2}sin(2x+\frac{π}{4})-1$,
当$x∈[0,\frac{π}{2}]$时,
$2x+\frac{π}{4}∈[\frac{π}{4},\frac{5π}{4}]$,
那么:$sin(2x+\frac{π}{4})∈[-\frac{{\sqrt{2}}}{2},1]$,
∴函数f(x)的值域为$[-2,\sqrt{2}-1]$.
(Ⅱ)由(Ⅰ)可得$f(x)=\sqrt{2}sin(2x+\frac{π}{4})-1$,
∵$f(C)=\sqrt{2}sin(2C+\frac{π}{4})-1=0$,
化简得:$sin(2C+\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,
又∵0<C<π,
∴$2C+\frac{π}{4}=\frac{3π}{4}$,
∴$C=\frac{π}{4}$
∵$acosB+bcosA=\frac{1}{2}{c^2}$,
由正弦定理,得$sinAcosB+sinBcosA=\frac{1}{2}csinC$;
∴$sin(A+B)=\frac{1}{2}csinC$,即$sinC=\frac{1}{2}csinC$;
又sinC>0,∴c=2.
∴$sinA=\frac{asinC}{c}=\frac{{\sqrt{2}×\frac{{\sqrt{2}}}{2}}}{2}=\frac{1}{2}$
∵a<c,∴$0<A<\frac{π}{4}$,$A=\frac{π}{6}$
∴$b=\frac{asinB}{sinA}=\frac{{\sqrt{2}sin(\frac{π}{4}+\frac{π}{6})}}{{\frac{1}{2}}}=1+\sqrt{3}$.
点评 本题考查了三角函数的化简能力以及性质的运用计算能力,同时考查了正弦定理的运用能力.属于基础题.


科目:高中数学 来源: 题型:解答题
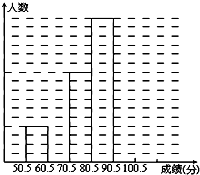 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | a | 0.16 |
| 70.5~80.5 | 10 | b |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | c | d |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {3,4} | D. | {x|1<x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{2}$,0) | B. | ($\frac{π}{4}$,0) | C. | ($\frac{π}{9}$,0) | D. | ($\frac{π}{16}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定存在正数d,使得b-a<c-d | B. | 一定存在正数d,使得a-c<b-d | ||
| C. | 对任意的正数d,有$\frac{1}{a}$-$\frac{1}{b}$<$\frac{1}{d}$-$\frac{1}{c}$ | D. | 对任意的正数d,有ad>bd>cd |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com