解:(1)∵数列{a
n}的前n项和
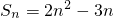
,
∴n≥2 时,a
n=S
n-S
n-1=4n-4,
当n=1时,a
1=S
1=-1,满足上式
∴数列{a
n}的通项公式为a
n=4n-5(n∈N
*)
∵数列{b
n}是正项等比数列,a
1=-b
1,b
3(a
2-a
1)=b
1.
∴b
1=1,b
3=

,q=

∴数列{b
n}的通项公式为b
n=

(2)∵c
n=a
nb
n,∴c
n=
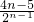
由
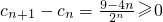
,可得n≤2,当n≥3时,c
n+1≤c
n∴c
3最大,最大值为

.
故存在正整数M,使得对一切n∈N
*,都有c
n≤M成立,M的最小值为2
分析:(1)当n=1时,a
1=S
1=-1,当n≥2时,利用a
n=S
n-S
n-1得到a
n的通项公式,把n=1代入也满足,得到即可;因为数列{bn}是各项为正的等比数列,根据a
1=-b
1,b
3(a
2-a
1)=b
1,即可利用等比数列的通项公式得到b
n的通项;
(2)把a
n和b
n的通项公式代入到c
n=a
nb
n中,可确定c
3最大,即可得到结论.
点评:本题考查数列的通项公式,考查数列的单调性,考查存在性问题,属于中档题.

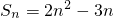 ,数列{bn}是正项等比数列,且a1=-b1,b3(a2-a1)=b1.
,数列{bn}是正项等比数列,且a1=-b1,b3(a2-a1)=b1.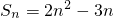 ,
, ,q=
,q=

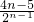
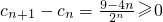 ,可得n≤2,当n≥3时,cn+1≤cn
,可得n≤2,当n≥3时,cn+1≤cn .
.
