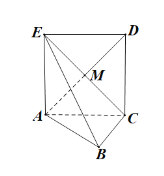
【题目】如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，
，且
（1）求证：
平面
；
（2）求三棱锥
的体积.
（3）求二面角
的大小.
【答案】（1）证明见解析.（2）
.（3）
【解析】
以点
为原点，以过点平行于
的直线为
轴，以
和
为
轴和
轴，建立空间直角坐标系
.
（1）根据线面垂直的判定定理，只要证
，
，则问题可证；
（2）由题意易得
平面
，所以将看成底面，
为高，利用等体积法求解.
（3）根据题意，求得平面
的一个法向量为
，又
为平面
的一个法向量，代入
求解.
四边形
是正方形，
，
平面
平面，
平面，
以点为原点，以过点平行于的直线为轴，以和为轴和轴，建立如图空间直角坐标系.
设
，则
，
，
，
，
是正方形的对角线的交点，
.
（1）
，
，
，
，
，
，
平面.
（2）
.
（3）设平面的一个法向量为，
则
且
，
且
.
， 即
取
，则
，则
.
又为平面的一个法向量，且
，
，
设二面角
的平面角为
，则
，
.
二面角
等于.
科目：高中数学 来源： 题型：
【题目】已知点
，
的两顶点
，且点
满足
（1）求动点的轨迹方程；
（2）设
，求动点
的轨迹方程；
（3）过点
的动直线
与曲线交于不同两点
，过点
作
轴垂线
，试判断直线与直线
的交点是否恒在一条定直线上？若是，求该定直线的方程，否则，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果数列
，
，…，
（m ≥ 3，
）满足：①＜＜…＜；②存在实数
，
，
，…，
和d，使得≤＜≤＜≤
＜…≤＜，且对任意0 ≤ i ≤ m﹣1（I 
），均有
，那么称数列，，…，是“Q数列”．
（1）判断数列1，3，6，10是不是“Q数列”，并说明理由；
（2）已知k，t均为常数，且k＞0，求证：对任意给定的不小于3的正整数m，数列
（n＝1，2，…，m）都是“Q数列”；
（3）若数列
（n＝1，2，…，m）是“Q数列”，求m的所有可能值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某医院用光电比色计检查尿汞时，得尿汞含量(毫克/升)与消光系数如下表：
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
（1）作散点图；
（2）如果
与
之间具有线性相关关系，求回归线直线方程；
（3）估计尿汞含量为9毫克/升时消光系数．
，
．
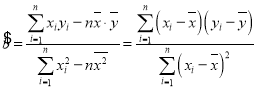参考数据：
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市规定，高中学生在校期间须参加不少于80小时的社区服务才合格．某校随机抽取20位学生参加社区服务的数据，按时间段
（单位：小时）进行统计，其频率分布直方图如图所示．
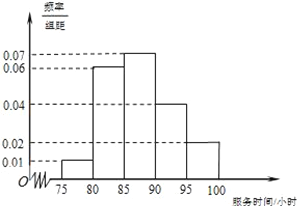
（1）求抽取的20人中，参加社区服务时间不少于90小时的学生人数；
（2）从参加社区服务时间不少于90小时的学生中任意选取2人，求所选学生的参加社区服务时间在同一时间段内的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市收集并整理了该市2019年1月份至10月份各月最低气温与最高气温(单位：℃)的数据，绘制了下面的折线图.（ ）
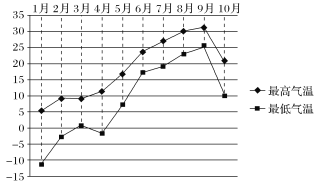
已知该城市各月的最低气温与最高气温具有较好的线性关系，则根据折线图，下列结论正确的是
A.最低气温与最高气温为正相关B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月D.最低气温低于0 ℃的月份有4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】圆周上依次排列着
共2013个不同的点，每个点染红、蓝、绿三色之一.在以任意两个同色点为端点的圆弧上，与此两端点异色的点的个数为偶数的染色方法称为“好染色”问：所有好染色方法有多少种？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（13分）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，O为AC中点，PO⊥平面ABCD，PO=2，M为PD中点．
（Ⅰ）证明：PB∥平面ACM；
（Ⅱ）证明：AD⊥平面PAC；
（Ⅲ）求直线AM与平面ABCD所成角的正切值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
