
分析 (1)容易得出$\overrightarrow{BD}=-5\overrightarrow{AB}$,从而$\overrightarrow{BD},\overrightarrow{AB}$共线,进而得出A,B,D三点共线;
(2)由$k\overrightarrow{a}+12\overrightarrow{b}$和$3\overrightarrow{a}+k\overrightarrow{b}$共线即可得到:$k\overrightarrow{a}+12\overrightarrow{b}=λ(3\overrightarrow{a}+k\overrightarrow{b})$,从而可得到关于k,λ的方程组,解出k即可.
解答 解:(1)$\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}$=$-3(\overrightarrow{a}-\overrightarrow{b})-2\overrightarrow{a}-13\overrightarrow{b}=-5\overrightarrow{a}-10\overrightarrow{b}$=$-5\overrightarrow{AB}$;
又AB,BD有公共点B;
∴A,B,D三点共线;
(2)∵$k\overrightarrow{a}+12\overrightarrow{b}$和$3\overrightarrow{a}+k\overrightarrow{b}$共线;
∴存在实数λ,使得$k\overrightarrow{a}+12\overrightarrow{b}=λ(3\overrightarrow{a}+k\overrightarrow{b})$;
∴$\left\{\begin{array}{l}{k=3λ}\\{12=kλ}\end{array}\right.$;
解得k=±6.
点评 考查向量加法的几何意义,向量的数乘运算,平面向量及共线向量基本定理.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
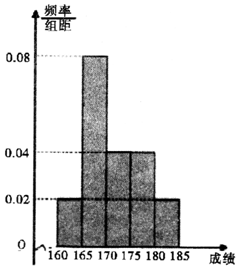 近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:
近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(\frac{x}{2}+\frac{π}{3})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=tan(x+\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设铁路AB长为100,BC⊥AB,且BC=30,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
设铁路AB长为100,BC⊥AB,且BC=30,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$或2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com