
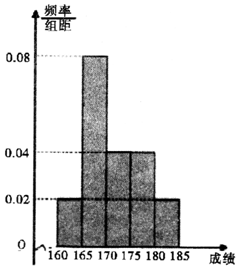
 近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:
近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:分析 (Ⅰ)首先求出第3,4,5组的频数,然后根据分层抽样中抽取的比例相等求出三组所抽取的人数;
(Ⅱ)利用列举法列出在5名选手中随机抽取2名选手的所有方法种数,查出第4组至少有一名选手被抽取的种数,然后直接利用古典概型概率计算公式求解.
解答 解:(Ⅰ)由频率分布直方图易知第3组的频率为0.04×(175-170)=0.2,从而第3组的频数为100×0.2=20,
同理可得第4、5组的频数分别为20、10,所以第3、4、5组共有50名选手.
利用分层抽样在50名选手中抽取5名选手,每组抽取的人数分别为:
第3组:$\frac{20}{50}$×5=2人,第4组:$\frac{20}{50}$×5=2人,第5组:$\frac{10}{50}$×5=1人,
所以第3、4、5组分别抽取2人、2人、1人.
(Ⅱ)设第3组的2位选手为A,B,第4组的2位选手为C,D,第5组的1位选手为E,则从这五位选手中抽取两位选手有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10种.
其中第4组的2位选手C,D中至少有一位选手入选的有:AC,BC,AD,BD,CD,CE,DE共有7种,
所以第4组至少有一名选手的概率为$\frac{7}{10}$
点评 本题考查了频率分布直方图,考查了古典概型及其概率计算公式,解答的关键是正确列出在5名学生中随机抽取2名学生的所有情况,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (1,2] | C. | (1,+∞) | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,e4) | D. | (e4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{13}$ | B. | $-\frac{24}{13}$ | C. | $\frac{10}{13}$ | D. | $-\frac{10}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com