
分析 (1)将2(a2-b2)=2accosB+bc化解结合余弦定理可得答案.
(2)因为∠DAC=$\frac{π}{2}$,所以AD=CD•sinC,∠DAB=$\frac{π}{6}$.利用正弦定理即可求解.
解答 解:(1)由题意2accosB=a2+c2-b2,
∴2(a2-b2)=a2+c2-b2+bc.
整理得a2=b2+c2+bc,
由余弦定理:a2=b2+c2-2bccosA
可得:bc=-2bccosA
∴cosA=-$\frac{1}{2}$,
∵0<A<π
∴A=$\frac{2π}{3}$.
(Ⅱ)∵∠DAC=$\frac{π}{2}$,
∴AD=CD•sinC,∠DAB=$\frac{π}{6}$.
在△ABD中,有$\frac{AD}{sinB}=\frac{BD}{sin∠DAB}$,
又∵CD=3BD,
∴3sinC=2sinB,
由C=$\frac{π}{3}$-B,得$\frac{{3\sqrt{3}}}{2}$cosB-$\frac{3}{2}$sinB=2sinB,
整理得:tanB=$\frac{{3\sqrt{3}}}{7}$.
点评 本题考查了正弦、余弦定理的灵活运用和计算能力.属于中档题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,4) | B. | (4,-2) | C. | (-4,6) | D. | (4,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (1,2] | C. | (1,+∞) | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
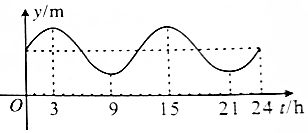
| A. | 6h | B. | 8h | C. | 12h | D. | 24h |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| 总计 | 21 | 19 | 40 |
| P(K≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A. | 有99%的把握认为环保知识测试成绩与专业有关 | |
| B. | 有99%的把握认为环保知识测试成绩与专业无关 | |
| C. | 有95%的把握认为环保知识测试成绩与专业无关 | |
| D. | 有95%的把握认为环保知识测试成绩与专业有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com