
 ��ͼ����֪A��10��0����ֱ��x=t��0��t��10���뺯��y=ex��ͼ���ڵ�P����x�ύ�ڵ�H���ǡ�APH�����Ϊf��t����
��ͼ����֪A��10��0����ֱ��x=t��0��t��10���뺯��y=ex��ͼ���ڵ�P����x�ύ�ڵ�H���ǡ�APH�����Ϊf��t�������� ��1��������֪AH=10-t��PH=et���Ӷ��ɵ�f��t��=$\frac{1}{2}$��10-t��et��0��t��10��
��2����$f'��t��=-\frac{1}{2}{e^t}+\frac{1}{2}����{10-t}��{e^t}=\frac{1}{2}{e^t}��{9-t}��$���Ӷ��ɵ���������ȷ�������ĵ����Լ���ֵ���ɣ�
��3������g��t��=$\left\{\begin{array}{l}{\frac{1}{2}��10-t��+\frac{1}{6}{t}^{3}-4��t��0}\\{bt��t��0}\end{array}\right.$���Ӷ��ɵ�t��0ʱg�䣨t��=$\frac{1}{2}$t2-$\frac{1}{2}$=$\frac{1}{2}$��t-1����t+1�����Ӷ��жϺ����ĵ����Լ���ֵ���ٽ�Ϸֶκ������Ӷ�ȷ��ʹ�÷���g��t��=m����ֻ������ʵ����ʱm��ȡֵ��Χ��
��� 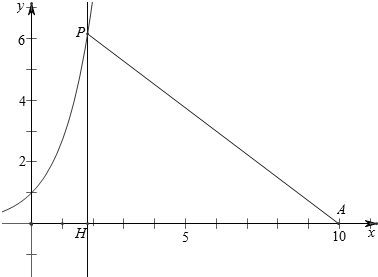 �⣺��1������֪��AH=10-t��PH=et��
�⣺��1������֪��AH=10-t��PH=et��
����f��t��=$\frac{1}{2}$��10-t��et��0��t��10��
��2���⣺$f'��t��=-\frac{1}{2}{e^t}+\frac{1}{2}����{10-t}��{e^t}=\frac{1}{2}{e^t}��{9-t}��$��
��f�䣨t��=0��t=9��
����f��t����f�䣨t���ڶ������ϵ�����±���
| t | ��0��9�� | 9 | ��9��10�� |
| f�䣨t�� | + | 0 | - |
| f��t�� | �J | ����ֵ | �K |
���� ���⿼���˵������ۺ�Ӧ�ü��ֶκ�����Ӧ�ã�ͬʱ���������ν�ϵ�˼��Ӧ�ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 1��-1 | D�� | ��1��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ǰ����� | B�� | Сǰ����� | ||
| C�� | ������ʽ���� | D�� | ��ǰ���Сǰ�ᶼ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
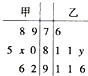 ij��ѧ��һ���Ӽס����������и�ѡ��7��ѧ���μ���ѧ����������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ�����мװ�ѧ���ɼ���������80���Ұ�ѧ���ɼ�����λ����89����x+y��ֵΪ��������
ij��ѧ��һ���Ӽס����������и�ѡ��7��ѧ���μ���ѧ����������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ�����мװ�ѧ���ɼ���������80���Ұ�ѧ���ɼ�����λ����89����x+y��ֵΪ��������| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ�������� | B�� | ���������� | C�� | ����ֱ�������� | D�� | �������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com