
【题目】已知向量a=![]() ,b=
,b=![]() ,且x∈
,且x∈![]() .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值是-![]() ,求λ的值.
,求λ的值.
【答案】见解析
【解析】解 (1)a·b=cos ![]() cos
cos ![]() -sin
-sin ![]() sin
sin ![]() =cos 2x,
=cos 2x,
|a+b|=![]()
=![]() =2
=2![]() ,
,
因为x∈![]() ,所以cos x≥0,
,所以cos x≥0,
所以|a+b|=2cos x.
(2)由(1),可得f(x)=a·b-2λ|a+b|=cos 2x-4λcos x,
即f(x)=2(cos x-λ)2-1-2λ2.
因为x∈![]() ,所以0≤cos x≤1.
,所以0≤cos x≤1.
①当λ<0时,当且仅当cos x=0时,f(x)取得最小值-1,这与已知矛盾;
②当0≤λ≤1时,当且仅当cos x=λ时,f(x)取得最小值-1-2λ2,由已知得-1-2λ2=-![]() ,解得λ=
,解得λ=![]() ;
;
③当λ>1时,当且仅当cos x=1时,f(x)取得最小值1-4λ,由已知得1-4λ=-![]() ,解得λ=
,解得λ=![]() ,这与λ>1相矛盾;综上所述λ=
,这与λ>1相矛盾;综上所述λ=![]() .
.


科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在![]() ,
,![]() 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在![]() 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①![]() ;②当
;②当![]() 时,
时, ![]() ;③
;③![]() ;④当
;④当![]() 秒时,
秒时, ![]() ∽
∽![]() ;⑤当
;⑤当![]() 的面积为
的面积为![]() 时,时间
时,时间![]() 的值是
的值是![]() 或
或![]() ;其中正确的结论是( )
;其中正确的结论是( )
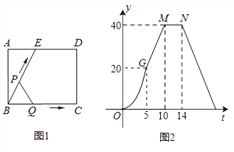
A. ①⑤ B. ②⑤ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
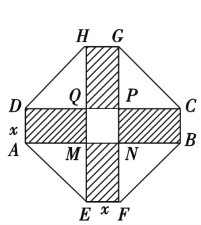
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
R(x)=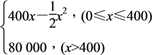
其中x是仪器的月产量.
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少元?(总收益=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
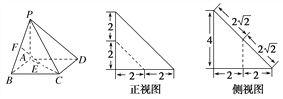
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com